题目内容
15.在长为1的线段AB上任取不同于A,B的两点C,D,则AC+BD>$\frac{1}{2}$的概率为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{9}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
分析 本题考查的知识点是几何概型,我们分别用x,y表示这两点到A的距离,则0<x<1且0<y<1,且x+1-y>$\frac{1}{2}$,即x-y>-$\frac{1}{2}$.我们可以先画出满足条件的所有的点对应的平面区域,分别求出对应平面区域的面积,然后代入几何概型计算公式即可求解.
解答 解:设任取两点所表示的数分别为x,y,则0<x<1且0<y<1,且x+1-y>$\frac{1}{2}$,即x-y>-$\frac{1}{2}$..
它表示的平面区域如下图中正方形所示,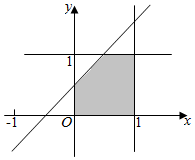
它对应的面积如图中阴影部分所示,
故AC+BD>$\frac{1}{2}$的概率为1-$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$=$\frac{7}{8}$;
故选:D.
点评 本题考查了几何概型的概率求法;关键是估算公式中的“几何度量”,可以为线段长度、面积、体积等表示.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5.已知θ∈($\frac{π}{2}$,π),sinθ+cosθ=-$\frac{{\sqrt{10}}}{5}$,则tan(θ-$\frac{π}{4}$)的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | -2 |
3.某高中计划从全校学生中按年级采用分层抽样方法抽取20名学生进行心理测试,其中高三有学生900人,已知高一与高二共抽取了14人,则全校学生的人数为( )
| A. | 2400 | B. | 2700 | C. | 3000 | D. | 3600 |
10.已知Sn是等差数列{an}的前n项和,S3+S6=18,则S5=( )
| A. | 14 | B. | 10 | C. | 9 | D. | 5 |
20.下列说法错误的是( )
| A. | 一个三棱柱可以由一个三棱锥和一个四棱锥拼合而成 | |
| B. | 一个圆台可以由两个圆台拼合而成 | |
| C. | 一个圆锥可以由两个圆锥拼合而成 | |
| D. | 一个四棱台可以由两个四棱台拼合而成 |
7.命题:“?x0∈R,x0>sinx0”的否定是( )
| A. | ?x∈R,x≤sinx | B. | ?x∈R,x>sinx | C. | ?x0∈R,x0<sinx0 | D. | ?x0∈R,x0≤sinx0 |
4.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点为F1、F2,上顶点A,离心率为$\frac{1}{2}$,点P为第一象限内椭圆上的一点,若S${\;}_{△P{F}_{1}A}$=4S${\;}_{△P{F}_{1}{F}_{2}}$,则直线PF1的斜率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{9}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{2\sqrt{3}}{9}$ |