题目内容
6.函数f(x)=$\frac{{x{{log}_a}|x|}}{|x|}$(0<a<1)图象的大致形状是( )| A. | 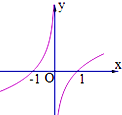 | B. | 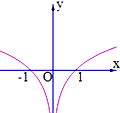 | C. | 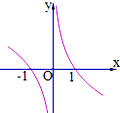 | D. | 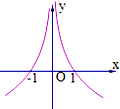 |
分析 确定函数是奇函数,图象关于原点对称,x>0时,f(x)=logax(0<a<1)是单调减函数,即可得出结论.
解答 解:由题意,f(-x)=-f(x),所以函数是奇函数,图象关于原点对称,排除B、D;
x>0时,f(x)=logax(0<a<1)是单调减函数,排除A.
故选:C.
点评 本题考查函数的图象,考查函数的奇偶性、单调性,正确分析函数的性质是关键.

练习册系列答案
相关题目
1.已知实数x,y满足$\left\{\begin{array}{l}{y≥1}\\{y≤2x-1}\\{x+y≤m}\end{array}\right.$,如果目标函数z=y-x的最大值为1,则实数m等于( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
11.已知函数fM(x)的定义域为实数集R,满足狄利克雷函数fM(x)=$\left\{\begin{array}{l}1,x∈M\\ 0,x∉M\end{array}$(M是R的非空真子集),在R上有两个非空真子集A,B,且A∩B=∅,则F(x)=$\frac{{{f_{A∪B}}(x)+1}}{{{f_A}(x)+{f_B}(x)+1}}$的值域为( )
| A. | (0,$\frac{2}{3}$] | B. | {1} | C. | {$\frac{1}{2}$,$\frac{2}{3}$,1} | D. | [$\frac{1}{3}$,1] |
18.已知复数z=-1-3i,则下列说法正确的是( )
| A. | z的虚部为3i | |
| B. | z的共轭复数为1-3i | |
| C. | |z|=4 | |
| D. | z在复平面内对应的点在第三象限内 |
15.在长为1的线段AB上任取不同于A,B的两点C,D,则AC+BD>$\frac{1}{2}$的概率为( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{9}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |