题目内容
5.已知θ∈($\frac{π}{2}$,π),sinθ+cosθ=-$\frac{{\sqrt{10}}}{5}$,则tan(θ-$\frac{π}{4}$)的值为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | -2 |
分析 由条件求得tan(θ-$\frac{π}{4}$)<-1,利用同角三角函数的基本关系求得sin2θ=cos($\frac{π}{2}$-2θ)的值,再利用二倍角的余弦公式求得tan(θ-$\frac{π}{4}$)的值.
解答 解:∵θ∈($\frac{π}{2}$,π),sinθ+cosθ=-$\frac{{\sqrt{10}}}{5}$,∴θ∈($\frac{3π}{4}$,π),∴θ-$\frac{π}{4}$∈($\frac{π}{2}$,$\frac{3π}{4}$),tan(θ-$\frac{π}{4}$)<-1.
故1+2sinθcosθ=$\frac{2}{5}$,∴sin2θ=cos($\frac{π}{2}$-2θ)=$\frac{{cos}^{2}(\frac{π}{4}-θ){-sin}^{2}(\frac{π}{4}-θ)}{{cos}^{2}(\frac{π}{4}-θ){+sin}^{2}(\frac{π}{4}-θ)}$=$\frac{1{-tan}^{2}(\frac{π}{4}-θ)}{1{+tan}^{2}(\frac{π}{4}-θ)}$=-$\frac{3}{5}$,
求得tan(θ-$\frac{π}{4}$)=±2,故tan(θ-$\frac{π}{4}$)=-2,
故选:D.
点评 本题主要考查同角三角函数的基本关系、二倍角的余弦公式的应用,属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
20.设x∈R,则“a=b”是“f(x)=(x+a)|x+b|为奇函数”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.i是虚数单位,复数$\frac{3+4i}{1-2i}$=( )
| A. | 1+2i | B. | 1-2i | C. | -1+2i | D. | -1-2i |
15.在长为1的线段AB上任取不同于A,B的两点C,D,则AC+BD>$\frac{1}{2}$的概率为( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{9}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
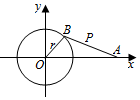 如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.
如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.