题目内容
3.某高中计划从全校学生中按年级采用分层抽样方法抽取20名学生进行心理测试,其中高三有学生900人,已知高一与高二共抽取了14人,则全校学生的人数为( )| A. | 2400 | B. | 2700 | C. | 3000 | D. | 3600 |
分析 设全校学生的人数为n和要抽取的样本容量,即可求出答案.
解答 解:设全校学生的人数为n,
则$\frac{20}{n}$=$\frac{20-14}{900}$,
解得n=3000,
故选:C
点评 分层抽样的方法步骤为:首先确定分层抽取的个数.分层后,各层的抽取一定要考虑到个体数目,选取不同的抽样方法,但一定要注意按比例抽取,其中按比例是解决本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
11.已知函数fM(x)的定义域为实数集R,满足狄利克雷函数fM(x)=$\left\{\begin{array}{l}1,x∈M\\ 0,x∉M\end{array}$(M是R的非空真子集),在R上有两个非空真子集A,B,且A∩B=∅,则F(x)=$\frac{{{f_{A∪B}}(x)+1}}{{{f_A}(x)+{f_B}(x)+1}}$的值域为( )
| A. | (0,$\frac{2}{3}$] | B. | {1} | C. | {$\frac{1}{2}$,$\frac{2}{3}$,1} | D. | [$\frac{1}{3}$,1] |
18.已知复数z=-1-3i,则下列说法正确的是( )
| A. | z的虚部为3i | |
| B. | z的共轭复数为1-3i | |
| C. | |z|=4 | |
| D. | z在复平面内对应的点在第三象限内 |
8.已知集合A={y|y=2x-1,x∈R},B={x|x-x2>0},则A∩B=( )
| A. | (-1,+∞) | B. | (-1,1) | C. | (-1,0) | D. | (0,1) |
15.在长为1的线段AB上任取不同于A,B的两点C,D,则AC+BD>$\frac{1}{2}$的概率为( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{9}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
13.在△ABC中,tanA+tanC=3tanB,则tanB的取值范围是( )
| A. | (0,+∞) | B. | [1,+∞) | C. | [$\frac{4}{3}$,+∞) | D. | [1,$\frac{4}{3}$] |
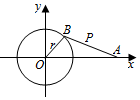 如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.
如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.