题目内容
 已知抛物线y2=2px(p>0)上点T(3,t)到焦点F的距离为4.
已知抛物线y2=2px(p>0)上点T(3,t)到焦点F的距离为4.(Ⅰ)求t,p的值;
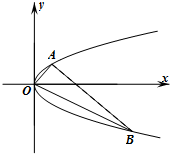
(Ⅱ)设A、B是抛物线上分别位于x轴两侧的两个动点,且
| OA |
| OB |
(ⅰ)求证:直线AB必过定点,并求出该定点P的坐标;
(ⅱ)过点P作AB的垂线与抛物线交于C、D两点,求四边形ACBD面积的最小值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用抛物线y2=2px (p>0)上点T(3,t)到焦点F的距离为4,根据抛物线的定义,可求t,p的值;
(Ⅱ)(ⅰ)设直线AB的方程为x=my+t,代入抛物线方程,利用韦达定理,结合
•
=5,可求t的值,即可求出该定点P的坐标;
(ⅱ)表示出四边形ACBD面积,令m2+
=μ(μ≥2),则S=8
是关于μ的增函数,即可求出四边形ACBD面积的最小值.
(Ⅱ)(ⅰ)设直线AB的方程为x=my+t,代入抛物线方程,利用韦达定理,结合
| OA |
| OB |
(ⅱ)表示出四边形ACBD面积,令m2+
| 1 |
| m2 |
| 5μ2+36μ+52 |
解答:
 (Ⅰ)解:由已知得3+
(Ⅰ)解:由已知得3+
=4⇒p=2,
所以抛物线方程为y2=4x,
代入可解得t=±2
.…(4分)
(Ⅱ)(ⅰ)证明:设直线AB的方程为x=my+t,A(
,y1)、B(
,y2),
联立
得y2-4my-4t=0,则y1+y2=4m,y1y2=-4t.…(6分)
由
•
=5得:
+y1y2=5⇒y1y2=-20或y1y2=4(舍去),
即-4t=-20⇒t=5,所以直线AB过定点P(5,0);…(10分)
(ⅱ)解:由(ⅰ)得|AB|=
|y2-y1|=
,
同理得|CD|=
|y2-y1|=
,
则四边形ACBD面积S=
|AB|•|CD|=
•
=8
令m2+
=μ(μ≥2),则S=8
是关于μ的增函数,
故Smin=96.当且仅当m=±1时取到最小值96.…(15分)
 (Ⅰ)解:由已知得3+
(Ⅰ)解:由已知得3+| p |
| 2 |
所以抛物线方程为y2=4x,
代入可解得t=±2
| 3 |
(Ⅱ)(ⅰ)证明:设直线AB的方程为x=my+t,A(
| ||
| 4 |
| ||
| 4 |
联立
|
由
| OA |
| OB |
| (y1y2)2 |
| 16 |
即-4t=-20⇒t=5,所以直线AB过定点P(5,0);…(10分)
(ⅱ)解:由(ⅰ)得|AB|=
| 1+m2 |
| 1+m2 |
| 16m2+80 |
同理得|CD|=
1+(-
|
1+
|
|
则四边形ACBD面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+m2 |
| 16m2+80 |
1+
|
|
(2+(m2+
|
令m2+
| 1 |
| m2 |
| 5μ2+36μ+52 |
故Smin=96.当且仅当m=±1时取到最小值96.…(15分)
点评:本题考查抛物线的方程,考查直线与抛物线的位置关系,考查四边形面积的计算,考查韦达定理的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图所示程序框图中,输出S=( )
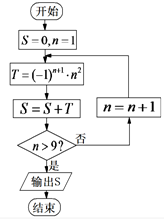

| A、45 | B、-55 |
| C、-66 | D、66 |
下列说法不正确的是( )
| A、方程f(x)=0有实数根?函数y=f(x)有零点 |
| B、函数y=-x2+3x+5有两个零点 |
| C、单调函数至多有一个零点 |
| D、函数f(x)在区间[a,b]上满足f(a)•f(b)<0,则函数f(x)在区间(a,b)内有零点 |
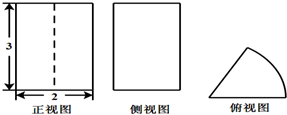 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的侧面积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的侧面积为( )A、12+
| ||
B、6+
| ||
| C、12+2π | ||
| D、6+4π |
