题目内容
9.等差数列{an}中,a1+a4+a7=48,a2+a5+a8=40,则a3+a6+a9的值是( )| A. | 30 | B. | 32 | C. | 34 | D. | 36 |
分析 由已知的第2个等式减去第1个等式,利用等差数列的性质得到差为公差d的3倍,且求出3d的值,然后再由所求式子减去第2个等式,利用等差数列的性质也得到其差等于3d,把3d的值代入即可求出所求式子的值.
解答 解:设等差数列的公差为d,
由a1+a4+a7=48①,a2+a5+a8=40②,
②-①得:(a2-a1)+(a5-a4)+(a8-a7)=3d=40-48=-8,
则(a3+a6+a9)-(a2+a5+a8)=(a3-a2)+(a6-a5)+(a9-a8)=3d=-8,
所以a3+a6+a9=(a2+a5+a8)+3d=40-8=32
故选B.
点评 此题考查学生掌握等差数列的性质,是一道基础题.解题的突破点是将已知的两等式相减.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
20.已知抛物线y=4ax2,则其准线方程是( )
| A. | y=-$\frac{1}{16a}$ | B. | x=-a | C. | y=±$\frac{1}{16a}$ | D. | x=±a |
19.已知角α的顶点在原点,始边与x轴的非负半轴重合,终边交以原点为圆心的单位圆于点A,将角α的终边按逆时针方向旋转$\frac{π}{6}$后交此单位圆于点B,记A(x1,y1),B(x2,y2),若A(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则x2的值为( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
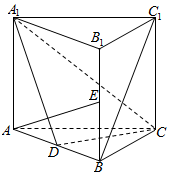 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.