题目内容
3.高三学生小罗利用暑假参加社会实践,为了帮助贸易公司的购物网站优化今年国庆节期间的营销策略,他对去年10月1日当天在该网站消费且消费金额不超过1000元的1000名(女性800名,男性200名)网购者,根据性别按分层抽样的方法抽取100名进行分析,得到如下统计图表(消费金额单位:元):| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
| 人数 | 5 | 10 | 15 | 47 | x |
男性消费情况:
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
| 人数 | 2 | 3 | 10 | y | 2 |
(Ⅱ)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写右面2×2列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
| 女性 | 男性 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
| P(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
分析 (Ⅰ)根据分层抽样方法求出x、y的值,利用列举法计算基本事件数,求出对应的概率;
(Ⅱ)列出2×2列联表,计算观测值K2,对照表中数据,判断结论是否成立即可.
解答 解:(Ⅰ)按分层抽样女性应抽取80名,男性应抽取20名.
∴x=80-(5+10+15+47)=3…(2分)
y=20-(2+3+10+2)=3…(3分)
抽出的100名且消费金额在[800,1000](单位:元)的网购者中有三位女性设为A,B,C;两位男性设为a,b,从5人中任选2人的基本事件有:(A,B),(A,C),(A,a),(A,b),(B,C),(B,a),(B,b),(C,a),(C,b),(a,b)共10件…(4分)
设“选出的两名网购者恰好是一男一女”为事件A
事件A包含的基本事件有:(A,a),(A,b),(B,a),(B,b),(C,a),(C,b)共6件…(5分)∴P(A)=$\frac{6}{10}$=$\frac{3}{5}$.
…(6分)
(Ⅱ)2×2列联表如下表所示
| 女性 | 男性 | 总计 | |
| 网购达人 | 50 | 5 | 55 |
| 非网购达人 | 30 | 15 | 45 |
| 总计 | 80 | 20 | 100 |
则k2=$\frac{100(50×15-30×5)^{2}}{80×20×55×45}$…(9分)≈9.091…(10分)
∵9.091>6.635且P(k2≥6.635)=0.010…(11分)
答:在犯错误的概率不超过0.010的前提下可以认为“是否为‘网购达人’”与性别有关…(12分)
点评 本题考查了分层抽样方法的应用问题,也考查了2×2列联表的应用问题,属于中档题.

练习册系列答案
相关题目
8.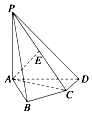 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(1)证明:AE⊥平面PCD;
(2)求PB和平面PAD所成的角的大小.
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.(1)证明:AE⊥平面PCD;
(2)求PB和平面PAD所成的角的大小.
15.若点P到点F(2,0)的距离比它到直线x+3=0的距离小1,则点P的轨迹方程是( )
| A. | y2=2x | B. | y2=4x | C. | y2=8x | D. | x2=8y |
13.若底面边长为$\sqrt{3}$,高为2$\sqrt{3}$的正三棱柱内接于半径为R的球O,则球O的半径R的值为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\sqrt{3}$ |