题目内容

10．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-2x，x≤0}\\{ln（2x-1），x＞0}\end{array}\right.$，则f（f（1））=（　　）
A．0B．1C．2D．3

分析 由已知中函数的解析式f（x）=$\left\{\begin{array}{l}{{x}^{2}-2x，x≤0}\\{ln（2x-1），x＞0}\end{array}\right.$，将x=1代入可得答案．

解答 解：∵f（x）=$\left\{\begin{array}{l}{{x}^{2}-2x，x≤0}\\{ln（2x-1），x＞0}\end{array}\right.$，
∴f（1）=0，
∴f（f（1））=f（0）=0，
故选：A

点评 本题考查的知识点是分段函数的应用，函数求值，难度不大，属于基础题．

练习册系列答案
相关题目
20．已知向量$\overrightarrow{a}$=（1，$\sqrt{3}$），$\overrightarrow{b}$=（3，m），且$\overrightarrow{b}$在$\overrightarrow{a}$上的投影为3，则向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角为$\frac{π}{6}$．
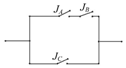1．如图，JA，JB两个开关串联再与开关JC并联，在某段时间内每个开关能够闭合的概率都是0.5，计算在这段时间内线路正常工作的概率为0.625．
18．已知f（x）=x2-ax+lnx，a∈R．
（1）若a=0，求函数y=f（x）在点（1，f（1））处的切线方程；
（2）若函数f（x）在[$\frac{1}{2}$，1]上是增函数，求实数a的取值范围；
（3）令g（x）=x2-f（x），x∈（0，e]（e是自然对数的底数）；求当实数a等于多少时，可以使函数g（x）取得最小值为3．
5．函数f（x）的导函数为f′（x），对?x∈R，都有2f′（x）＞f（x）成立，若f（ln4）=2，则不等式f（x）＞e${\;}^{\frac{x}{2}}}$的解集是（　　）
A．（1，+∞）B．（0，ln4）C．（ln4，+∞）D．（0，1）
15．在锐角△ABC 中，A，B，C的对边为a，b，c，A=2B，则$\frac{a}{b}$的取值范围是（$\sqrt{2}$，$\sqrt{3}$）．
2．求适合下列条件的椭圆的标准方程：
（1）焦点在x轴上，且经过点（2，0）和点（0，1）；
（2）焦点在y轴上，与y轴的一个交点为P（0，-10），P到它较近的一个焦点的距离等于2．
19．（1）已知f（x+1）=x2-3x+2，求f（x）的解析式．
（2）二次函数f（x）满足f（x+1）-f（x）=2x，且f（0）=1，求f（x）的解析式．
20．已知△ABC的内角A，B，C所对的边分别为a，b，c，且向量$\overrightarrow m$=（cos2B-1，2sinA）与向量$\overrightarrow n$=（$\sqrt{2}$sinC，-1）平行．
（1）若a=$\sqrt{2}$，b=1，求c；
（2）若$\frac{c}{a}$+$\frac{a}{c}$＞4sin（A+C），求cosB的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网