题目内容
20.已知向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=(3,m),且$\overrightarrow{b}$在$\overrightarrow{a}$上的投影为3,则向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角为$\frac{π}{6}$.分析 根据$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影是|$\overrightarrow{b}$|×cosθ,列出方程求出m的值,再计算$\overrightarrow{a}$、$\overrightarrow{b}$的夹角θ的值.
解答 解:∵$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为3,
且|$\overrightarrow{a}$|=$\sqrt{{1}^{2}{+(\sqrt{3})}^{2}}$=2,$\overrightarrow{a}$•$\overrightarrow{b}$=3+$\sqrt{3}$m;
∴|$\overrightarrow{b}$|×cosθ=|$\overrightarrow{b}$|×$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{3+\sqrt{3}m}{2}$=3;
解得m=$\sqrt{3}$,
∴|$\overrightarrow{b}$|=2$\sqrt{3}$;
∴cosθ=$\frac{3}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
由θ∈[0,π],
∴$\overrightarrow{a}$、$\overrightarrow{b}$的夹角θ为$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题考查向量在另一个向量上的投影定义及计算公式,向量夹角的应用问题,是基础题目.

练习册系列答案
相关题目
10.已知f(x)=a-$\frac{2}{{2}^{x}+1}$(a∈R)是奇函数,那么实数a的值等于( )
| A. | 1 | B. | -1 | C. | 0 | D. | ±1 |
5.为了得到函数y=$\sqrt{2}$cos3x的图象,可以将函数y=sin3x+cos3x的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{12}$个单位 |
9.若函数f(x)满足f(x)+2f($\frac{1}{x}$)=3x,则f(2)的值为( )
| A. | -1 | B. | 2 | C. | 3 | D. | $\frac{1}{2}$ |
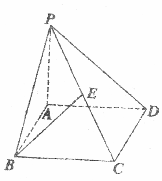 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a.
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a. 如图,在边长为2的正方形中随机撒1000粒豆子,有180粒落到阴影部分,据此估计阴影部分的面积为0.72.
如图,在边长为2的正方形中随机撒1000粒豆子,有180粒落到阴影部分,据此估计阴影部分的面积为0.72.