题目内容
5.函数f(x)的导函数为f′(x),对?x∈R,都有2f′(x)>f(x)成立,若f(ln4)=2,则不等式f(x)>e${\;}^{\frac{x}{2}}}$的解集是( )| A. | (1,+∞) | B. | (0,ln4) | C. | (ln4,+∞) | D. | (0,1) |
分析 构造函数g(x)=$\frac{f(x)}{{e}^{\frac{x}{2}}}$,利用导数可判断g(x)的单调性,再根据f(ln4)=2,求得g(ln4)=1,继而求出答案
解答 解:∵?x∈R,都有2f′(x)>f(x)成立,
∴f′(x)-$\frac{1}{2}$f(x)>0,于是有($\frac{f(x)}{{e}^{\frac{x}{2}}}$)′>0,
令g(x)=$\frac{f(x)}{{e}^{\frac{x}{2}}}$,则有g(x)在R上单调递增,
∵不等式f(x)>e${\;}^{\frac{x}{2}}}$,
∴g(x)>1,
∵f(ln4)=2,
∴g(ln4)=1,
∴x>ln4,
故选:C.
点评 本题考查导数的运算及利用导数研究函数的单调性,属中档题,解决本题的关键是根据选项及已知条件合理构造函数,利用导数判断函数的单调性.

练习册系列答案
相关题目
10.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-2x,x≤0}\\{ln(2x-1),x>0}\end{array}\right.$,则f(f(1))=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
17.已知sinθ+cosθ=2sinα,sin2θ=2sin2β,则( )
| A. | cosβ=2cosα | B. | cos2β=2cos2α | C. | cos2β+2cos2α=0 | D. | cos2β=2cos2α |
14.若l、m、n是互不重合的直线,α、β是不重合的平面,则下列命题中为真命题的是( )
| A. | 若α⊥β,l?α,n?β,则l⊥n | B. | 若l⊥α,l∥β,则α⊥β | ||
| C. | 若l⊥n,m⊥n,则l∥n | D. | 若α⊥β,l?α,则l⊥β |
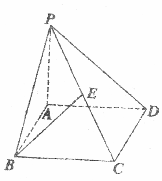 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a.
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=$\frac{{\sqrt{6}}}{3}$a.