题目内容
已知命题p:-10≤x≤2,q:x2-2x+1-a2≥0(a>0),若非p是q的充分不必要条件,求a的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:求出不等式的等价条件,根据充分条件和必要条件的定义即可得到结论.
解答:
解:∵p:-10≤x≤2,∴¬p:x>2或x<-10,
q:x2-2x+1-a2≥0(a>0),解得x≥1+a或x≤1-a,
∵非p是q的充分不必要条件,
∴,
即
,
解得0<a≤1.
q:x2-2x+1-a2≥0(a>0),解得x≥1+a或x≤1-a,
∵非p是q的充分不必要条件,
∴,
|
|
解得0<a≤1.
点评:本题主要考查充分条件和必要条件的判断,根据不等式的性质求出对应的解是解决本题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
若函数f(x)=sin2x-cos2x+sin2x-m在[0,
]上有零点,则实数m的取值范围为( )
| π |
| 4 |
A、[-1,
| ||
| B、[-1,1] | ||
C、[1,
| ||
D、[-
|
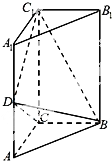 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=2,BC=4,AA1=4,D是棱AA1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=2,BC=4,AA1=4,D是棱AA1的中点.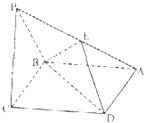 己知如图,四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°.又PC⊥平面ABCD,PC=a.E为PA的中点.
己知如图,四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°.又PC⊥平面ABCD,PC=a.E为PA的中点.