题目内容
2．已知点P（m，n）是抛物线x2=16y上的一点，抛物线的焦点为F，若|PF|=5，则|mn|=4．分析 根据抛物线上的点到焦点和准线的距离相等，可得n，m值．
解答 解：∵抛物线x2=16y上一点P（m，n），F为抛物线的焦点，|PF|=5，
∴n+4=5，
解得：n=1，m2=16，可得m=±4，
|mn|=4．
故答案为：4．
点评 本题考查的知识点是抛物线的简单性质，难度不大，属于基础题．
练习册系列答案
相关题目
10．某几何体的三视图如图，则该几何体的体积为（ ）
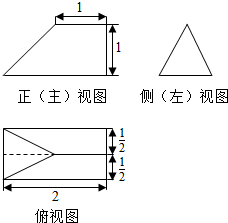
| A． | $\frac{5}{6}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
11．棱长为1的正方体ABCD-A1B1C1D1中，$\overrightarrow{A{B_1}}•\overrightarrow{B{C_1}}$的值为（ ）
| A． | -1 | B． | 1 | C． | $\sqrt{2}$ | D． | 2 |
某学生对其30位亲属的饮食习惯进行了一次调查，并用茎叶图表示30人的饮食指数．说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主．