题目内容
已知数列{an}的前n项和Sn=n2+4n(n∈N*).
(1)求数列{an}的通项公式;
(2)若b1=3,且bn+1-bn=an(n∈N*),求数列{
}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)若b1=3,且bn+1-bn=an(n∈N*),求数列{
| 1 |
| bn |
考点:数列的求和,数列递推式
专题:点列、递归数列与数学归纳法
分析:(1)根据数列项an与Sn之间的关系即可得到结论.
(2)利用累加法先求出数列{bn}的通项公式,然后利用分组求和法即可求数列{
}的前n项和Tn.
(2)利用累加法先求出数列{bn}的通项公式,然后利用分组求和法即可求数列{
| 1 |
| bn |
解答:
解:(1)当n=1时,a1=S1=12+4=5,
当n≥2,an=Sn-Sn-1=n2+4n-(n-1)2-4(n-1)=2n+3,
综上an=2n+3,(n∈N*);
(2)∵bn+1-bn=an=2n+3,
∴bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)=3+5+7+…+(2n+1)=
×n=n(n+2),
由(1)得:
=
=
(
-
),
∴Tn=
(1-
+
-
+…+
-
+
-
)=
(1+
-
-
)
=
-
,n∈N*).
当n≥2,an=Sn-Sn-1=n2+4n-(n-1)2-4(n-1)=2n+3,
综上an=2n+3,(n∈N*);
(2)∵bn+1-bn=an=2n+3,
∴bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)=3+5+7+…+(2n+1)=
| 3+2n+1 |
| 2 |
由(1)得:
| 1 |
| bn |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 3 |
| 4 |
| 2n+3 |
| 2(n+1)(n+2) |
点评:本题主要考查数列的通项公式以及数列求和,利用裂项法以及累加法是解决本题的关键.

练习册系列答案
相关题目
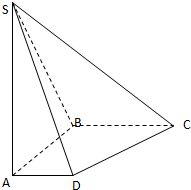 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=