题目内容
9.已知双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$,以C的右焦点F为圆心,以a为半径的圆与C的一条渐近线交于A,B两点,若△ABF为等边三角形,则双曲线C的离心率为( )| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{2}$ |
分析 根据直线和圆相交时的弦长公式结合双曲线离心率的公式进行转化求解即可.
解答 解:∵双曲线的一个焦点为F(c,0),双曲线的一条渐近线为y=$\frac{b}{a}$x,即bx-ay=0,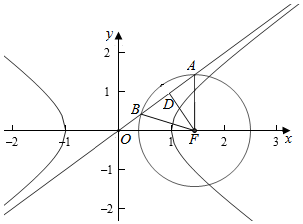
∴焦点到渐近线的距离d=$\frac{|bc|}{\sqrt{{a}^{2}+{b}^{2}}}$=b,
∵|AF|=|BF|=a,△ABF为等边三角形,
∴|AB|=2|AD|=2$\sqrt{{a}^{2}-{b}^{2}}$=a,
平方得4(a2-b2)=a2,
即a2-c2+a2=$\frac{1}{4}$a2,
则$\frac{7}{4}$a2=c2,
即离心率e=$\frac{\sqrt{7}}{2}$,
故选:A
点评 本题主要考查双曲线离心率的计算,根据直线和圆相交的弦长公式建立方程关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.在实数集R中定义一种运算“⊙”,具有性质:①对任意a、b∈R,a⊙b=b⊙a;②a⊙0=a;③对任意a、b∈R,(a⊙b)⊙c=(ab)⊙c+(a⊙c)+(b⊙c)-2c,则函数f(x)=x⊙$\frac{1}{x}({x>0})$的最小值是( )
| A. | 2 | B. | 3 | C. | $3\sqrt{2}$ | D. | $2\sqrt{2}$ |
20.“x<2”是“-3<x<2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
17.已知随机变量ξ的分布列为(如表所示):设η=2ξ+1,则η的数学期望Eη的值是$\frac{2}{3}$.
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{2}$ | $\frac{1}{6}$ | $\frac{1}{3}$ |
4.命题p:?x<0,2x>x,命题q:?x∈R,x2+x+1<0,则下列命题正确的是( )
| A. | (¬p)∨q为真 | B. | p∨q为真 | C. | p∧(¬q)为假 | D. | (¬p)∧(¬q)为真 |
1.若实数a,b满足$\frac{1}{a}+\frac{1}{b}=\sqrt{ab}$,则ab的最小值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
18.某校共有学生3000名,各年级男、女生人数如表所示,已知高一、高二年级共有男生1120人,现用分层抽样的方法在全校抽取60名学生,则应在高三年级抽取的学生人数为( )
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 456 | 424 | y |
| 男生 | 644 | x | z |
| A. | 16 | B. | 18 | C. | 20 | D. | 24 |
 在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),离心率e=$\frac{{\sqrt{2}}}{2}$.
在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),离心率e=$\frac{{\sqrt{2}}}{2}$.