题目内容
19.在实数集R中定义一种运算“⊙”,具有性质:①对任意a、b∈R,a⊙b=b⊙a;②a⊙0=a;③对任意a、b∈R,(a⊙b)⊙c=(ab)⊙c+(a⊙c)+(b⊙c)-2c,则函数f(x)=x⊙$\frac{1}{x}({x>0})$的最小值是( )| A. | 2 | B. | 3 | C. | $3\sqrt{2}$ | D. | $2\sqrt{2}$ |
分析 根据题中给出的对应法则,可得f(x)=(x⊙$\frac{1}{x}$)⊙0=1+x+$\frac{1}{x}$,利用基本不等式求最值可得x+≥$\frac{1}{x}$2,当且仅当x=1时等号成立,由此可得函数f(x)的最小值为f(1)=3.
解答 解:根据题意,得
f(x)=x⊙$\frac{1}{x}$=(x⊙$\frac{1}{x}$)⊙0=0⊙(x•$\frac{1}{x}$)+(x⊙0)+($\frac{1}{x}$⊙0)-2×0=1+x+$\frac{1}{x}$
即f(x)=1+x+$\frac{1}{x}$,
∵x>0,可得x+$\frac{1}{x}$≥2,当且仅当x=1时等号成立,由此可得函数f(x)的最小值为f(1)=3.
故选:B
点评 本题给出新定义,求函数f(x)的最小值.着重考查了利用基本不等式求最值、函数的解析式求法和简单的合情推理等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知圆C1:x2+y2-2mx+m2=4,圆C2:x2+y2+2x-2my=8-m2(m>3),则两圆的位置关系是( )
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 外离 |
14.设$a={({\frac{1}{2}})^{\frac{1}{2}}},b={({\frac{1}{2}})^{\frac{1}{3}}},c={log_{\frac{1}{2}}}2$,则( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
8.已知F1、F2分别是双曲线$\frac{x^2}{8}-{y^2}$=1的左、右焦点,P为双曲线右支上的一点,I是△PF1F2的内心,且${S_{△IP{F_2}}}={S_{△IP{F_1}}}-m{S_{△I{F_1}{F_2}}}$,则m=( )
| A. | $\frac{{2\sqrt{14}}}{7}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{{3\sqrt{2}}}{4}$ | D. | $\frac{1}{3}$ |
9.已知双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$,以C的右焦点F为圆心,以a为半径的圆与C的一条渐近线交于A,B两点,若△ABF为等边三角形,则双曲线C的离心率为( )
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{2}$ |
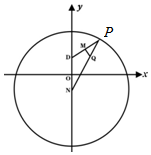 如图,已知圆N:x2+(y+$\sqrt{5}$)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,$\sqrt{5}$)和DP上的点M,满足$\overrightarrow{DP}$=2$\overrightarrow{DM}$,$\overrightarrow{MQ}$•$\overrightarrow{DP}$=0.
如图,已知圆N:x2+(y+$\sqrt{5}$)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,$\sqrt{5}$)和DP上的点M,满足$\overrightarrow{DP}$=2$\overrightarrow{DM}$,$\overrightarrow{MQ}$•$\overrightarrow{DP}$=0.