题目内容
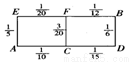
(本题14分)张老师居住在某城镇的A处,准备开车到学校B处上班。若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图。(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为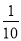 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为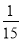 )。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量
)。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量 ,求
,求 的数学期望
的数学期望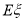 。
。
(1)路线A→C→F→B,可使得途中发生堵车事件的概率最小;(2) 。
。
【解析】
试题分析:(1)分别求出路线A→C→D→B、路线A→E→F→B、A→C→F→B遇到堵车的概率,比较求出其中最小的, 以路线A→C→D→B遇到堵车的概率为例,可先求出路线A→C→D→B没有遇到堵车的概率;(2)路线A→C→F→B中遇到堵车次数 可取值为0,1,2,3,
可取值为0,1,2,3,
 =0时,没有堵车;
=0时,没有堵车; =1时,有一段堵车,;
=1时,有一段堵车,; =2时,,有两段堵车;
=2时,,有两段堵车; =3时,三段均堵车,期望
=3时,三段均堵车,期望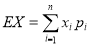 求出即可.
求出即可.
试题解析:(1)记路段AC发生堵车事件为AC,其余同此表示法。因为各路段发生堵车事件是独立的,且在同一路段发生堵车事件最多只有一次,所以路线A→C→D→B中遇到堵车的概率P1为
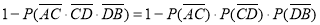
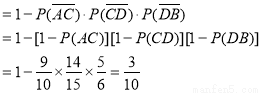
同理:路线A→C→F→B中遇到堵车的概率P2为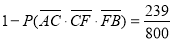
路线A→E→F→B中遇到堵车的概率P3为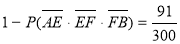
显然要使得A到B的路线途中发生堵车事件的概率最小,只可能在以上三条路线中选择。又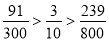
因此选择路线A→C→F→B,可使得途中发生堵车事件的概率最小
(2)路线A→C→F→B中遇到堵车次数 可取值为0,1,2,3
可取值为0,1,2,3

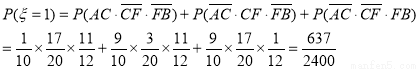
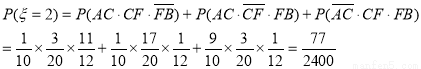

所以
故路线A→C→F→B中遇到堵车次数的数学期望为
考点:1、对立时间的概率;2、离散型随机变量的分布列、期望.

练习册系列答案
相关题目
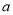 为大于
为大于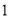 的常数,函数
的常数,函数 ,若关于
,若关于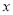 的方程
的方程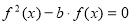 恰有三个不同的实数解,则实数
恰有三个不同的实数解,则实数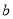 的取值范围是 .
的取值范围是 . ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )



 ,
,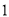 ,
,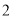 ,…,
,…,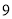 这十个数字组成的无重复数字的四位数中,十位数字与千位数字之差的绝对值等于
这十个数字组成的无重复数字的四位数中,十位数字与千位数字之差的绝对值等于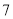 的四位数的个数是 .
的四位数的个数是 . 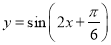 的图象向左平移
的图象向左平移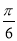 个单位,再向上平移
个单位,再向上平移 个单位,所得图象的函数解析式是( )
个单位,所得图象的函数解析式是( )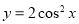 B.
B.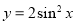
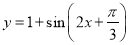 D.
D.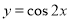
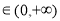 ,|r|越大,相关程度越大;反之相关程度越小
,|r|越大,相关程度越大;反之相关程度越小 ,|r|越大,相关程度越大;反之相关程度越小
,|r|越大,相关程度越大;反之相关程度越小 ,且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小
,且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小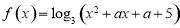 ,
,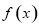 在区间
在区间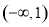 上是递减函数,则实数
上是递减函数,则实数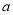 的取值范围为_________.
的取值范围为_________.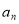 }的前n项和为
}的前n项和为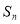 ,且
,且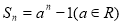 ,则{
,则{ ,
,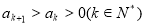 ,则对于任意自然数
,则对于任意自然数 ,都有
,都有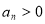 ;
;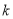 ,使
,使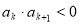 ,则对于任意
,则对于任意 ,都有
,都有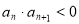 ,
,