题目内容

求y=
8
x2-5x+4
的值域．
考点：函数的值域
专题：函数的性质及应用
分析：由题意，可对分母配方，求出分母的取值范围，再令t=x2-5x+4，则函数变为y=
8
t
，t≥-
9
4
，利用反比例函数的性质求出值域．
解答： 解：由于x2-5x+4=(x-
5
2
)2-
9
4
≥-
9
4
，
令t=x2-5x+4，则函数变为y=
8
t
，t≥-
9
4
；
由反比例函数的性质知，y∈（-∞，-
32
9
）∪（0，+∞），
故函数y=
8
x2-5x+4
的值域为（-∞，-
32
9
）∪（0，+∞）．
点评：本题可查求函数的值域，对于此类复合函数值域的求法，可由内而外表层来求
练习册系列答案
相关题目
若an是（2+x）n（n∈N*，n≥2，x∈R）展开式中x2项的系数，则
lim
n→∞
(
22
a2
+
23
a3
+…+
2n
an
)=
 
．
已知下列4个结论中其中正确的序号是 （　　）
A、已知cosα=
1
3
，cos（α+β）=1则cos（2α+β）的值为
1
3
B、已知2a=3b=k（k≠1）且2a+b=ab，则实数k的值为36
C、已知函数f(x)=
x2-1，x≥0
-1，x＜0
，则满足不等式f（2-x2）＞f（3x）的x的取值范围是(-
2
，
-3+
17
2
)
D、已知函数f（x）对任意x，y都有f（x+y）=f（x）+f（y）-1，且当x＞0时，f（x）＞1，若关于x的不等式f（x2-ax+b）＜1的解集为{x|-3＜x＜2}，则a+b=-7
某班优秀生16人，中等生24人，学困生8人，现采用分层抽样的方法从这些学生中抽取6名学生做学习习惯调查，
（Ⅰ）求应从优秀生、中等生、学困生中分别抽取的学生人数；
（Ⅱ）若从抽取的6名学生中随机抽取2名学生做进一步数据分析，
（1）列出所有可能的抽取结果；
（2）求抽取的2名学生均为中等生的概率．
已知圆C过点M（0，-2），N（3，1），且圆心C在直线x+2y+1=0上．
（Ⅰ）求圆C的方程；
（Ⅱ）问是否存在满足以下两个条件的直线l：①斜率为1；②直线被圆C截得的弦为AB，以AB为直径的圆C1过原点．若存在这样的直线，请求出其方程；若不存在，说明理由．
甲乙两个地区高三年级分别有33000人，30000人，为了了解两个地区全体高三年级学生在该地区二模考试的数学成绩情况，采用分层抽样方法从两个地区一共抽取了105名学生的数学成绩，并作出了如下的频数分布统计表，规定考试成绩在[120，150]内为优秀．
甲地区：
分组[70，80）[80，90）[90，100）[100，110）
频数231015
分组[110，120）[120，130）[130，140）[140，150]
频数15x31
乙地区：
分组[70，80）[80，90）[90，100）[100，110）
频数1298
分组[110，120）[120，130）[130，140）[140，150]
频数1010y3
（Ⅰ）计算x，y的值；
（Ⅱ）根据抽样结果分别估计甲地区和乙地区的优秀率；若将此优秀率作为概率，现从乙地区所有学生中随机抽取3人，求抽取出的优秀学生人数ξ的数学期望；
（Ⅲ）根据抽样结果，从样本中优秀的学生中随机抽取3人，求抽取出的甲地区学生人数η的分布列及数学期望．
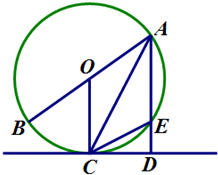如图，已知AB是⊙O的直径，CD是⊙O的切线，C为切点，连接AC，过点A作AD⊥CD于点D，交⊙O于点E．
（Ⅰ）证明：∠AOC=2∠ACD；
（Ⅱ）证明：AB•CD=AC•CE．
求函数y=x+
1-x2
的值域．
设l，m是两条不同的直线，α，β是两个不同的平面，有下列命题：
①l∥m，m?α，则l∥α；
②l∥α，m∥α则l∥m；
③α⊥β，l?α，则l⊥β；
④l⊥α，m⊥α，则l∥m．
其中正确的命题的个数是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网