题目内容
19.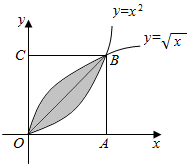 如图所示,在边长为1的正方形OABC中任取一点M,则点M恰好取自阴影部分的概率为$\frac{1}{3}$.
如图所示,在边长为1的正方形OABC中任取一点M,则点M恰好取自阴影部分的概率为$\frac{1}{3}$.
分析 由定积分公式计算阴影部分的面积,进而由几何概型公式计算可得答案.
解答 解:根据题意,正方形OABC的面积为1×1=1,
由函数y=x与y=$\sqrt{x}$围成阴影部分的面积为∫01($\sqrt{x}$-x)dx=($\frac{2}{3}{x}^{\frac{3}{2}}$-$\frac{{x}^{2}}{2}$)|01=$\frac{1}{6}$,
由于y=x2与y=$\sqrt{x}$互为反函数,所以阴影部分的面积为$\frac{1}{3}$,
则正方形OABC中任取一点P,点P取自阴影部分的概率为$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查几何概型的计算,涉及定积分在求面积中的应用,利用积分的几何意义正确计算出阴影部分的面积是解决本题的关键..

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表.某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
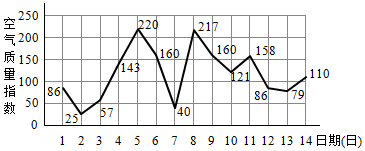
(Ⅰ)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(Ⅱ)求此人到达当日空气质量优良的概率;
(Ⅲ)设X是此人出差期间(两天)空气质量中度或重度重度污染的天数,求X的分布列与数学期望.

(Ⅰ)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(Ⅱ)求此人到达当日空气质量优良的概率;
(Ⅲ)设X是此人出差期间(两天)空气质量中度或重度重度污染的天数,求X的分布列与数学期望.
| 空气质量指数 | 污染程度 |
| 小于100 | 优良 |
| 大于100且小于150 | 轻度 |
| 大于150且小于200 | 中度 |
| 大于200且小于300 | 重度 |
| 大于300且小于500 | 严重 |
| 大于500 | 爆表 |
7.命题“?n∈N*,$\frac{1}{n}$>$\frac{1}{n+1}$”的否定为( )
| A. | ?n∈N*,$\frac{1}{n}$≤$\frac{1}{n+1}$ | B. | ?n∈N*,$\frac{1}{n}$<$\frac{1}{n+1}$ | ||
| C. | ?n∈N*,$\frac{1}{{n}_{0}}$≤$\frac{1}{{n}_{0}+1}$ | D. | ?n0∈N*,$\frac{1}{{n}_{0}}$<$\frac{1}{{n}_{0}+1}$ |
11.已知等差数列{an}的前n项和为Sn,若$\overrightarrow{OB}$=a4$\overrightarrow{OA}$+a2013$\overrightarrow{OC}$,且A,B,C三点共线(O为该直线外一点),则S2016等于( )
| A. | 2016 | B. | 1008 | C. | 22016 | D. | 21008 |
8.已知不重合的直线m、l和平面α、β,m⊥α,l?β,则α∥β是“m⊥l”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |