题目内容
8.设方程$\left\{\begin{array}{l}{x=1+cosθ}\\{y=\sqrt{3}+sinθ}\end{array}\right.$(θ为参数)表示的曲线为C.(1)求曲线C上的动点到原点O的距离的最小值;
(2)点P为曲线C上的动点,当|OP|最小时(O为坐标原点),求点P的坐标.
分析 (1)根据两点间的距离公式得出距离关于θ的函数,利用三角函数的性质得出距离的最小值;
(2)将(1)中的θ值代入参数方程解出P点坐标.
解答 解:(1)设曲线C上的点到原点得距离为d,
则d2=x2+y2=(1+cosθ)2+($\sqrt{3}$+sinθ)2=5+2cosθ+2$\sqrt{3}$sinθ=5+4sin(θ+$\frac{π}{6}$).
∴当sin(θ+$\frac{π}{6}$)=-1时,d2取得最小值1,
∴d的最小值为1.
(2)由(1)知当θ+$\frac{π}{6}$=-$\frac{π}{2}$+2kπ即θ=-$\frac{2π}{3}$+2kπ时,|OP|最小.
∴x=1+cos(-$\frac{2π}{3}$+2kπ)=$\frac{1}{2}$,y=$\sqrt{3}$+sin(-$\frac{2π}{3}$+2kπ)=$\frac{\sqrt{3}}{2}$.
∴P点坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
点评 本题考查了参数方程的应用,距离公式,三角函数的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.设i是虚数单位,若复数z满足(2-5i)z=29,则z=( )
| A. | 2-5i | B. | 2+5i | C. | -2-5i | D. | -2+5i |
13.下列函数中,周期为π的是( )
| A. | y=sin(2x-$\frac{π}{6}$) | B. | y=sin(x-$\frac{π}{6}$) | C. | y=cos(x-$\frac{π}{4}$) | D. | y=tan(2x+$\frac{π}{3}$) |
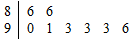 如图是某班8位学生诗词比赛得分的茎叶图,那么这8位学生得分的众数和中位数分别为93、92.
如图是某班8位学生诗词比赛得分的茎叶图,那么这8位学生得分的众数和中位数分别为93、92.