题目内容
9.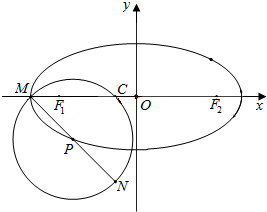 已知椭圆E的方程:$\frac{x^2}{100}+\frac{y^2}{25}=1$,P为椭圆上的一点(点P在第三象限上),圆P 以点P为圆心,且过椭圆的左顶点M与点C(-2,0),直线MP交圆P与另一点N.
已知椭圆E的方程:$\frac{x^2}{100}+\frac{y^2}{25}=1$,P为椭圆上的一点(点P在第三象限上),圆P 以点P为圆心,且过椭圆的左顶点M与点C(-2,0),直线MP交圆P与另一点N.(Ⅰ)求圆P的标准方程;
(Ⅱ)若点A在椭圆E上,求使得$\overrightarrow{AM}•\overrightarrow{AN}$取得最小值的点A的坐标;
(Ⅲ)若过椭圆的右顶点的直线l上存在点Q,使∠MQN为钝角,求直线l斜率的取值范围.
分析 (Ⅰ)设点P(m,n),利用$m=\frac{-10+(-2)}{2}=-6$,以及椭圆方程求出m,n,然后求出半径,即可求解圆的方程.
(Ⅱ)由题意求出N的坐标,设A(x,y),表示出$\overrightarrow{AM}•\overrightarrow{AN}$,求出最小值时点A的坐标.
( III)设直线l:y=k(x-10),利用直线与圆相交,圆心P到直线l的距离小于半径,列出不等式求解即可.
解答 解:(Ⅰ)椭圆E的方程:$\frac{x^2}{100}+\frac{y^2}{25}=1$,得M(-10,0),C(-2,0)…(1分)
设点P(m,n),则有$m=\frac{-10+(-2)}{2}=-6$,
又:$\frac{m^2}{100}+\frac{n^2}{25}=1$,∴n=-4,即P(-6,-4),…(2分)
所以$r=PM=4\sqrt{2}$---------------------------------------------------(3分)
所以圆P的标准方程为(x+6)2+(y+4)2=32----------------------------(4分)
(Ⅱ)∵P为MN的中点,可得N(-2,-8)
设A(x,y),∴$\overrightarrow{AM}=({-10-x,-y}),\overrightarrow{AN}=({-2-x,-8-y})$,∴$\overrightarrow{AM}•\overrightarrow{AN}=({-10-x})({-2-x})+({-y})({-8-y})={x^2}+12x+20+{y^2}+8y$---------(9分)∴$\overrightarrow{AM}•\overrightarrow{AN}={({x+6})^2}+{({y+4})^2}-32≥-32$,
得x=-6,y=-4时,∴$\overrightarrow{AM}•\overrightarrow{AN}$最小---------------------------------(7分)
经检验,点A在椭圆$\frac{x^2}{100}+\frac{y^2}{25}=1$上∴A(-6,-4)--------------------------(8分)
( III)设直线l:y=k(x-10),即直线与圆相交------------------------------(9分)
所以圆心P到直线l的距离$d=\frac{{|{-6k+4-10k}|}}{{\sqrt{1+{k^2}}}}<4\sqrt{2}$--------------------------(10分)
得$\frac{{|{1-4k}|}}{{\sqrt{1+{k^2}}}}<\sqrt{2}$
得$\frac{{4-\sqrt{30}}}{14}<k<\frac{{4+\sqrt{30}}}{14}$--------------------------(12分)
点评 本题考查直线与椭圆的标准方程的综合应用,圆的方程的综合应用,考查转化思想以及计算能力.

| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>a>b |
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | 48 | B. | 24 | C. | 12 | D. | 6 |
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
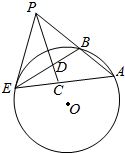 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D.
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D.