题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,满足c=1,且cosBsinC+(a-sinB)cos(A+B)=0
(1)求C的大小;
(2)求a2+b2的最大值,并求取得最大值时角A,B的值.
(1)求C的大小;
(2)求a2+b2的最大值,并求取得最大值时角A,B的值.
考点:余弦定理的应用
专题:三角函数的求值,解三角形
分析:(1)利用三角形的内角转化为A的三角函数,利用两角和的正弦函数求解结合正弦定理求出表达式,求出结合即可.
(2)由余弦定理以及基本不等式求解最值即可.
(2)由余弦定理以及基本不等式求解最值即可.
解答:
解:(1)cosBsinC+(a-sinB)cos(A+B)=0
可得:cosBsinC-(a-sinB)cosC=0
即:sinA-acosC=0.
由正弦定理可知:
=
,
∴
-acosC=0,
∴asinC-acosC=0,
sinC-cosC=0,可得
sin(C-
)=0,C是三角形内角,
∴C=
.
(2)由余弦定理可知:c2=a2+b2-2abcosC,
得1=a2+b2-
ab
又ab≤
,
∴(1-
)(a2+b2)≤1,
即:a2+b2≤2+
.
当A=B=
π时,a2+b2取到最大值为2+
.
可得:cosBsinC-(a-sinB)cosC=0
即:sinA-acosC=0.
由正弦定理可知:
| a |
| sinA |
| c |
| sinC |
∴
| asinC |
| c |
∴asinC-acosC=0,
sinC-cosC=0,可得
| 2 |
| π |
| 4 |
∴C=
| π |
| 4 |
(2)由余弦定理可知:c2=a2+b2-2abcosC,
得1=a2+b2-
| 2 |
又ab≤
| a2+b2 |
| 2 |
∴(1-
| ||
| 2 |
即:a2+b2≤2+
| 2 |
当A=B=
| 3 |
| 8 |
| 2 |
点评:本题考查三角形的最值,余弦定理的应用,正弦定理的应用,考查计算能力.

练习册系列答案
相关题目
(1-
)5的展开式x2的系数是( )
| x |
| A、-5 | B、5 | C、-10 | D、10 |
已知函数f(x)=
,若f(m)>f(-m),则实数m的取值范围是( )
|
| A、(-1,0)∪(0,1) |
| B、(-∞,-1)∪(1,+∞) |
| C、(-1,0)∪(1,+∞) |
| D、(-∞,-1)∪(0,1) |
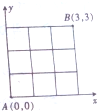 如图,电子青蛙从点A(0,0)出发,每跳一步只向上或右跳一单位长度,设每跳一步相互独立,且向上或向右的概率都为
如图,电子青蛙从点A(0,0)出发,每跳一步只向上或右跳一单位长度,设每跳一步相互独立,且向上或向右的概率都为