题目内容
已知x1,x2是关于x的方程x2+mx-(2m+1)=0的两个实数根,则经过两点A(x1,x12),B(x2,x22)的直线与椭圆
+
=1公共点的个数是( )
| x2 |
| 16 |
| y2 |
| 4 |
| A、2 | B、1 | C、0 | D、不确定 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:令m=0,求出x1,x2,进而求出A,B坐标,进而可分析出经过两点A(x1,x12),B(x2,x22)的直线与椭圆
+
=1公共点的个数,可得答案.
| x2 |
| 16 |
| y2 |
| 4 |
解答:
解:当m=0时,方程x2+mx-(2m+1)=0可化为:x2-1=0,
故x1=-1,x2=1,
故A,B两点的坐标为(-1,1),(1,1),
此时A,B两点均在椭圆
+
=1内部,故直线AB与椭圆
+
=1有2个公共点,
故选:A
故x1=-1,x2=1,
故A,B两点的坐标为(-1,1),(1,1),
此时A,B两点均在椭圆
| x2 |
| 16 |
| y2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
故选:A
点评:本题考查的知识点是直线与圆锥曲线的关系,本题为选择题,故可采用特殊值代入的方法求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在三菱锥P-ABC中,△ABC为等边三角形,PA⊥平面ABC,且PA=AB,则二面角A-PB-C的平面角的正切值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题中正确的是( )
| A、如果平面α⊥平面β,那么平面α内一定不存在直线平行于平面β |
| B、平面α⊥平面β,且α∩β=l,若在平面α内过任一点P做L的垂线m,那么m⊥平面β |
| C、如果平面α⊥平面γ,平面β⊥平面γ,那么平面α∥平面β |
| D、如果直线l∥平面α,那么直线l平行于平面α内的任意一条直线 |
 如图是一算法的程序框图,若此程序运行结果为s=28,则在判断框中应填入关于k的判断条件是( )
如图是一算法的程序框图,若此程序运行结果为s=28,则在判断框中应填入关于k的判断条件是( )| A、k<9 | B、k<8 |
| C、k<7 | D、k<6 |
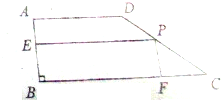 有一块形状为直角梯形的材料ABCD,底边BC的长为5米,边AB的长为1米(其中0<t<
有一块形状为直角梯形的材料ABCD,底边BC的长为5米,边AB的长为1米(其中0<t<