题目内容
(1)在△ABC中,角A,B,C所对边分别为a,b,c,若a+c=1,∠B=30°,求b的取值范围.
(2)在△ABC中,角A,B,C所对边分别为a,b,c,若b=4,∠B=60°,求S△ABC的最大值.
(2)在△ABC中,角A,B,C所对边分别为a,b,c,若b=4,∠B=60°,求S△ABC的最大值.
考点:余弦定理的应用,正弦定理
专题:解三角形
分析:(1)利用余弦定理列出关系式,通过基本不等式求解即可.
(2)利用余弦定理、基本不等式的性质、三角形面积的公式即可得出.
(2)利用余弦定理、基本不等式的性质、三角形面积的公式即可得出.
解答:
解:(1)在△ABC中,角A,B,C所对边分别为a,b,c,若a+c=1,∠B=30°,
由余弦定理可得:b2=a2+c2-2accosB=a2+c2-
ac=(a+c)2-(2+
)ac=1-(2+
)ac,
∵ac≤(
)2
∴ac≤
,当且仅当a=c=
时等号成立.
可得b2≥1-
=
.∴b≥
,b<a+c=1,
b的取值范围:[
,1).
(2)由余弦定理可得b2=a2+c2-2accosB,
∴16=a2+c2-2accos60°=a2+c2-ac≥2ac-ac=ac.当且仅当a=c时即思想是正三角形时,取等号.
∴S△ABC=
acsin60°≤
×16×
=4
.
∴△ABC面积的最大值为4
.
由余弦定理可得:b2=a2+c2-2accosB=a2+c2-
| 3 |
| 3 |
| 3 |
∵ac≤(
| a+c |
| 2 |
∴ac≤
| 1 |
| 4 |
| 1 |
| 2 |
可得b2≥1-
2+
| ||
| 4 |
2-
| ||
| 4 |
| ||||
| 4 |
b的取值范围:[
| ||||
| 4 |
(2)由余弦定理可得b2=a2+c2-2accosB,
∴16=a2+c2-2accos60°=a2+c2-ac≥2ac-ac=ac.当且仅当a=c时即思想是正三角形时,取等号.
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴△ABC面积的最大值为4
| 3 |
点评:本题考查余弦定理以及基本不等式的应用,考查计算能力.

练习册系列答案
相关题目
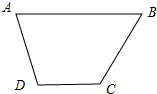 如图,等腰梯形ABCD中,AB∥CD,且AB=2,AD=1,DC=2x(x∈(0,1)),以A,B为焦点,且过点D的双曲线的离心率为e1.以C,D为焦点,且过点A的椭圆的离心率为e1,动点E在边AB上,且|AE|<e1+e2,对x∈(0,1)恒成立,则|AE|的最大值为( )
如图,等腰梯形ABCD中,AB∥CD,且AB=2,AD=1,DC=2x(x∈(0,1)),以A,B为焦点,且过点D的双曲线的离心率为e1.以C,D为焦点,且过点A的椭圆的离心率为e1,动点E在边AB上,且|AE|<e1+e2,对x∈(0,1)恒成立,则|AE|的最大值为( )