题目内容
在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),则|AB|= .
考点:空间向量的夹角与距离求解公式
专题:空间向量及应用
分析:利用空间中两点间距离公式求解.
解答:
解:∵点A(1,0,2),B(1,-3,1),
∴|AB|=
=
.
故答案为:
.
∴|AB|=
| (1-1)2+(-3-0)2+(1-2)2 |
| 10 |
故答案为:
| 10 |
点评:本题考查两点间距离的求法,是中档题,解题时要认真审题,注意空间中两点间距离公式的合理运用.

练习册系列答案
相关题目
把五进制数33(5)化成二进制数是( )
| A、100100(2) |
| B、10010(2) |
| C、1010(2) |
| D、10100(2) |
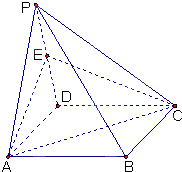 如图,四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且CD⊥面PAD,E 为侧棱PD的中点.
如图,四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且CD⊥面PAD,E 为侧棱PD的中点.