题目内容
已知各项都是正数的等比数列{an}满足7a4+3a3=7a2+3a1+4,那么7a8+3a7的最小值为 .
考点:等比数列的通项公式
专题:导数的综合应用,等差数列与等比数列
分析:设等比数列{an}的公比为q,则q>0且q≠1,根据题意用q表示出7a2+3a1,求出它的最小值即可.
解答:
解:设各项都是正数的等比数列{an}的公比为q,则q>0,
∵7a4+3a3=7a2+3a1+4,∴q≠1,
∴q2(7a2+3a1)=7a2+3a1+4,∴7a2+3a1=
;
∴7a8+3a7=q6(7a2+3a1)=
=
,
令
=t,则t>0,
∴
=
;
设f(t)=t2-t3,(t>0),
∴f′(t)=2t-3t2,
令f′(t)=0,
解得t=0(舍去),或t=
;
∴当t=
时,f(t)取得最大值是f(t)max=(
)2-(
)3=
,
∴
取得最小值是
=27.
故答案为:27.
∵7a4+3a3=7a2+3a1+4,∴q≠1,
∴q2(7a2+3a1)=7a2+3a1+4,∴7a2+3a1=
| 4 |
| q2-1 |
∴7a8+3a7=q6(7a2+3a1)=
| 4q6 |
| q2-1 |
| 4 | ||||
|
令
| 1 |
| q2 |
∴
| 4q6 |
| q2-1 |
| 4 |
| t2-t3 |
设f(t)=t2-t3,(t>0),
∴f′(t)=2t-3t2,
令f′(t)=0,
解得t=0(舍去),或t=
| 2 |
| 3 |
∴当t=
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 27 |
∴
| 4q6 |
| q2-1 |
| 4 | ||
|
故答案为:27.
点评:本题考查了等比数列的通项公式的应用问题,也考查了利用导数求函数的最值问题,是综合性题目.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
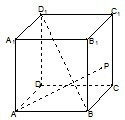 如图,正方体ABCD-A1B1C1D1的棱长为1,点P在侧面CBB1C1及其边界上运动,并且总保持B1P∥平面A1BD,则动点P的轨迹的长度是
如图,正方体ABCD-A1B1C1D1的棱长为1,点P在侧面CBB1C1及其边界上运动,并且总保持B1P∥平面A1BD,则动点P的轨迹的长度是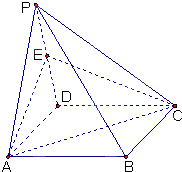 如图,四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且CD⊥面PAD,E 为侧棱PD的中点.
如图,四棱锥P-ABCD的底面是矩形,侧面PAD是正三角形,且CD⊥面PAD,E 为侧棱PD的中点.