题目内容
在直角坐标系内，到点（1，0）和直线x=-1距离相等的点的轨迹方程是 ．
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：由抛物线的定义可得，轨迹是以点（1，0）为焦点，以直线x=-1为准线的抛物线，即可写出抛物线方程．
解答：
解：在平面直角坐标系xOy中，到点（1，0）和直线x=-1距离相等的动点的轨迹是以点（1，0）为焦点，以直线x=-1为准线的抛物线，
∴p=2，
故抛物线方程为y2=4x，
故答案为：y2=4x．
∴p=2，
故抛物线方程为y2=4x，
故答案为：y2=4x．
点评：本题考查抛物线的定义、标准方程，以及简单性质的应用，判断轨迹是以点（1，0）为焦点，以直线x=-1为准线的抛物线，是解题的关键．
练习册系列答案
相关题目
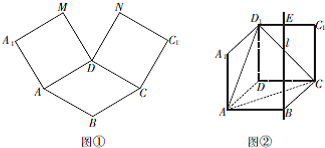如图①，在平面内，ABCD是∠BAD=60°且AB=a的菱形，ADMA1和CDNC1都是正方形． 将两个正方形分别沿AD，CD折起，使M与N重合于点D1．设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图②）．
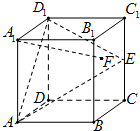在正方体ABCD-A1B1C1D1中，E是棱CC1的中点，F是侧面BCC1B1内的动点，且A1F∥平面D1AE，则A1F与平面BCC1B1所成角的正切值的取值范围是设函数f(x)=sin(ωx+
)(ω＞0)的最小正周期为π，则f（x）（ ）
| π |
| 2 |
A、在(0，
| ||||
B、在(
| ||||
C、在(0，
| ||||
D、在(
|
如图，正方体ABCD-A1B1C1D1的棱长为| 3 |
A、
| ||
B、
| ||
| C、π | ||
D、
|