题目内容
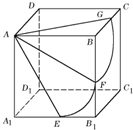
如图，正方体ABCD-A1B1C1D1的棱长为| 3 |
A、
| ||
B、
| ||
| C、π | ||
D、
|
考点：球内接多面体
专题：计算题,空间位置关系与距离,球
分析：球面与正方体的六个面都相交，所得的交线分为两类：一类在顶点A所在的三个面上，即面AA1B1B、面ABCD和面AA1D1D上；另一类在不过顶点A的三个面上，即面BB1C1C、面CC1D1D和面A1B1C1D1上．由空间几何知识能求出这两段弧的长度之和．
解答：
解：如图，球面与正方体的六个面都相交，
所得的交线分为两类：一类在顶点A所在的三个面上，即面AA1B1B、面ABCD和面AA1D1D上；
另一类在不过顶点A的三个面上，即面BB1C1C、面CC1D1D和面A1B1C1D1上．
在面AA1B1B上，交线为弧EF且在过球心A的大圆上，因为AE=2，AA1=
，
则∠A1AE=
．同理∠BAF=
，所以∠EAF=
，
故弧EF的长为：2×
=
，
而这样的弧共有三条．
在面BB1C1C上，交线为弧FG且在距球心为1的平面与球面相交所得的小圆上，
此时，小圆的圆心为B，半径为1，∠FBG=
，
所以弧FG的长为：1×
=
．
于是，所得的曲线长为：
+
=
．
故选：A．
所得的交线分为两类：一类在顶点A所在的三个面上，即面AA1B1B、面ABCD和面AA1D1D上；
另一类在不过顶点A的三个面上，即面BB1C1C、面CC1D1D和面A1B1C1D1上．
在面AA1B1B上，交线为弧EF且在过球心A的大圆上，因为AE=2，AA1=
| 3 |
则∠A1AE=
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
故弧EF的长为：2×
| π |
| 6 |
| π |
| 3 |
而这样的弧共有三条．
在面BB1C1C上，交线为弧FG且在距球心为1的平面与球面相交所得的小圆上，
此时，小圆的圆心为B，半径为1，∠FBG=
| π |
| 2 |
所以弧FG的长为：1×
| π |
| 2 |
| π |
| 2 |
于是，所得的曲线长为：
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
故选：A．
点评：本题考查空间几何的性质和综合应用，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知正方体ABCD-A1B1C1D1，截去三个角A-BDA1，C-BDC1，B1-BA1C1后形成的几何体的体积与原正方体的体积之比值为长方体三个面的面对角线的长度分别为3，3，
那么它的外接球的表面积为（ ）
| 14 |
| A、8π | B、16π |
| C、32π | D、64π |
已知i为虚数单位，则复数2i（1+i）的模是（ ）
| A、4 | ||
B、2
| ||
C、3
| ||
| D、8 |