题目内容
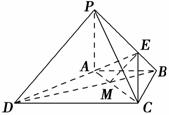
如图,在四棱锥P ABCD中,PA⊥底面ABCD,PC⊥AD,底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC,点E在棱PB上,且PE=2EB.
(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC.
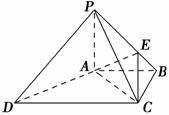
解 (1)∵PA⊥底面ABCD,∴PA⊥BC,
又AB⊥BC,PA∩AB=A,∴BC⊥平面PAB.(3分)
又BC⊂平面PCB,
∴平面PAB⊥平面PCB.(6分)
(2)∵PA⊥底面ABCD,又AD⊂平面ABCD,
∴PA⊥AD.
又∵PC⊥AD,又PC∩PA=P,∴AD⊥平面PAC,又AC⊂平面PAC,
∴AC⊥AD.
在梯形ABCD中,由AB⊥BC,AB=BC,得∠BAC=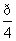 ,
,
∴∠DCA=∠BAC=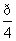 .又AC⊥AD,故△DAC为等腰直角三角形.(4分)
.又AC⊥AD,故△DAC为等腰直角三角形.(4分)
 ∴DC=
∴DC=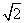 AC=
AC=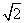 (
(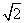 AB)=2AB.
AB)=2AB.
连接BD,交AC于点M,则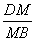 =
=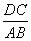 =2.
=2.
在△BPD中,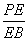 =
=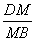 =2,
=2,
∴PD∥EM
又PD⊄平面EAC,EM⊂平面EAC,
∴PD∥平面EAC.(14分)

下表是某市从3月份中随机抽取的10天空气质量指数(AQI)和“PM2.5”(直径小于等于2.5微米的颗粒物)24小时平均浓度的数据,空气质量指数(AQI)小于100表示空气质量优良.
| 日期编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 空气质量指数(AQI) | 179 | 40 | 98 | 124 | 29 | 133 | 241 | 424 | 95 | 89 |
| “PM2.5”24小时平均浓度( | 135 | 5 | 80 | 94 | 80 | 100 | 190 | 387 | 70 | 66 |
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件M为“抽取的两个日期中,当天‘PM2.5’的24小时平均浓度不超过75 ”,求事件M发生的概率;
”,求事件M发生的概率;
(3)在上表数据中,在表示空气质量优良的日期中,随机抽取3天,记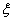 为“PM2.5”24小时平均浓度不超过75
为“PM2.5”24小时平均浓度不超过75 的天数,求
的天数,求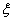 的分布列和数学期望.
的分布列和数学期望.
 ,且
,且 与
与 的夹角余弦为
的夹角余弦为 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.


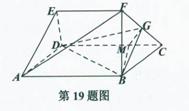
 2,CD=4,E为边DC的中点,如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.
2,CD=4,E为边DC的中点,如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.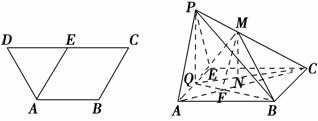
 拟投资开发某种新能源
拟投资开发某种新能源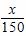 +2是否符合公司要求的奖励函数模型,并说明原因;
+2是否符合公司要求的奖励函数模型,并说明原因;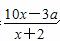 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值.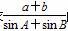 的值;
的值; 0),集合N={x|l-x<0},则集合M
0),集合N={x|l-x<0},则集合M (CRN)等于( )
(CRN)等于( )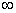 ) C.[-l,4) D.(1,4]
) C.[-l,4) D.(1,4]