题目内容
下表是某市从3月份中随机抽取的10天空气质量指数(AQI)和“PM2.5”(直径小于等于2.5微米的颗粒物)24小时平均浓度的数据,空气质量指数(AQI)小于100表示空气质量优良.
| 日期编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 空气质量指数(AQI) | 179 | 40 | 98 | 124 | 29 | 133 | 241 | 424 | 95 | 89 |
| “PM2.5”24小时平均浓度( | 135 | 5 | 80 | 94 | 80 | 100 | 190 | 387 | 70 | 66 |
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件M为“抽取的两个日期中,当天‘PM2.5’的24小时平均浓度不超过75 ”,求事件M发生的概率;
”,求事件M发生的概率;
(3)在上表数据中,在表示空气质量优良的日期中,随机抽取3天,记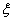 为“PM2.5”24小时平均浓度不超过75
为“PM2.5”24小时平均浓度不超过75 的天数,求
的天数,求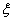 的分布列和数学期望.
的分布列和数学期望.
解:(1)由上表数据知,10天中空气质量指数(AQI)小于100的日期有:
A2 、A3 、A5 、A9 、A10共5天,故可估计该市当月某日空气质量优良的概率 .
.
(2)由(1)知10天中表示空气质量为优良的天数为5,当天“PM2.5”的24小时平均浓度不超过75 有编号为A2 、A9 、A10,共3天,
有编号为A2 、A9 、A10,共3天,
故事件M发生的概率 .
.
(3)由(1)知,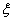 的可能取值为1,2,3.
的可能取值为1,2,3.
且

 ,
,
故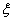 的分布列为:
的分布列为:
|
| 1 | 2 | 3 |
|
|
|
|
|
 的数学期望
的数学期望 .
.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目




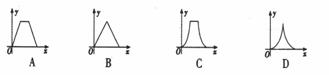
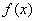 的图象大致是( )
的图象大致是( )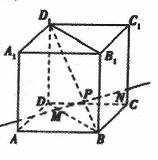
 :函数
:函数 是最小正周期为
是最小正周期为 的周期函数,命题
的周期函数,命题 :函数
:函数 在
在 上单调递减,则下列命题为真命题的是
上单调递减,则下列命题为真命题的是 B.
B. C.
C. D.
D. 

 等于
等于 B.
B.  C.
C. D.
D.
 其中
其中 表示不超过
表示不超过 的最大整数,
的最大整数, ,
, ,
, ).若直线
).若直线 与函数
与函数 的图象恰有三个不同的交点,则实数
的图象恰有三个不同的交点,则实数 的取值范围是
的取值范围是  B.
B. C.
C.  D.
D.
 (B)
(B) (C)
(C) (D)
(D)

 ,已知
,已知 ,那么△ABC一定是
,那么△ABC一定是