题目内容
在等腰梯形ABCD中,AB∥CD,AB=BC=AD= 2,CD=4,E为边DC的中点,如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.
2,CD=4,E为边DC的中点,如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.
(1)若PA∥平面MQB,求PM∶MC;
(2)若平面AEP⊥平面ABCE,点M是PC的中点,求三棱锥A MQB的体积.
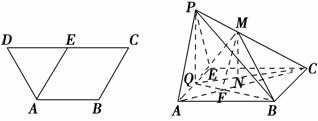
图1 图2
解 (1)连AC、BQ,设AC∩BQ=F,连MF.
则平面PAC∩平面MQB=MF,因为PA∥平面MQB,PA⊂平面PAC,所以PA∥MF.(2分)
在等腰梯形ABCD中,E为边DC的中点,所以由题设,AB=EC=2.
所以四边形ABCE为平行四边形,则AE∥BC.(4分)
从而△AFQ∽△CFB,AF∶FC=AQ∶CB=1∶2.
又PA∥MF,所以△FMC∽△APC,所以PM∶MC=AF∶FC=1∶2.(7分)
(2)由(1)知,△AED是边长为2的正三角形,从而PQ⊥AE.
因为平面AEP⊥平面ABCE,交线为AE,所以PQ⊥平面ABCE,PQ⊥QB,且PQ=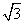 .
.
因为PQ⊂平面PQC,所以平面PQC⊥平面ABCE,交线为QC.(9分)
过点M作MN⊥QC于N,则MN⊥平面ABCE,所以MN是三棱锥M ABQ的高.
因为PQ⊥平面ABCE,MN⊥平面ABCE, 所以PQ∥MN.
所以PQ∥MN.
因为点M是PC的中点,所以MN=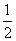 PQ=
PQ=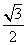 .(11分)
.(11分)
由(1)知,△ABE为正三角形,且边长为2.所以,S△ABQ=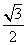 .
.
三棱锥A MQB的体积VA MQB=VM ABQ=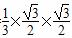 =
=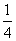 .
.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 F2=________.
F2=________.
 各棱长都为a,p为线段
各棱长都为a,p为线段 上的动点.
上的动点. ;
; 的大小;
的大小;
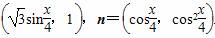 (1)若m·n=1,求cos
(1)若m·n=1,求cos 的值;
的值; b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.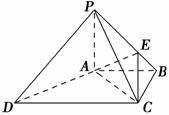
 =1的焦点到渐近线的距离为( )
=1的焦点到渐近线的距离为( ) :函数
:函数 是最小正周期为
是最小正周期为 的周期函数,命题
的周期函数,命题 :函数
:函数 在
在 上单调递减,则下列命题为真命题的是
上单调递减,则下列命题为真命题的是 B.
B. C.
C. D.
D. 