题目内容
14.已知圆O1:(x+1)2+(y-1)2=25与圆O2:(x-5)2+(y-b)2=65相交,且公共弦长为8,求b的值.分析 连结两圆圆心,则由垂径定理可求出圆心距,根据两点间的距离列方程求出b.
解答 解:设两圆交于A,B两点,AB中点为C,则O1A=5,O2A=$\sqrt{65}$,AC=4,
∴O1C=$\sqrt{{5}^{2}-{4}^{2}}$=3,O2C=$\sqrt{65-{4}^{2}}$=7,
∵O1(-1,1),O2(5,b),∴O1O2=$\sqrt{(-1-5)^{2}+({1-b)}^{2}}$=10.
∴b=-7或9.
点评 本题考查了圆与圆的位置关系,垂径定理,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
2.如图是一正方体,则其缩小的展开图是( )
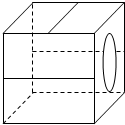

| A. |  | B. | 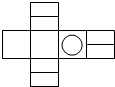 | C. | 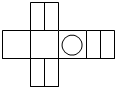 | D. |  |
3.已知点A(2,-1,5),B(t,t+1,t-1),则|AB|取得最小值时,t的值等于( )
| A. | $\sqrt{15}$ | B. | 3$\sqrt{2}$ | C. | $\sqrt{30}$ | D. | 2 |