Question

3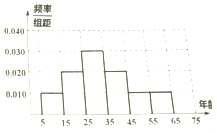．2016年3月31日贵州省第十二届人民代表大会常务委员会第二十一次会议通过的《贵州省人口与计划生育条例》全面开放二孩政策．为了了解人们对于贵州省新颁布的“生育二孩放开”政策的热度，现在某市进行调查，对[5，65]岁的人群随机抽取了n人，得到如下统计表和各年龄段抽取人数频率分布直方图：

分组	支持“生育二孩”人数	占本组的频率
[5，15）	4	0.8
[15，25）	5	p
[2，35）	12	0.8
[35，45）	8	0.8
[45，55）	2	0.4
[55，65）	1	0.2

（1）求n，p的值；
（2）根据以上统计数据填下面2×2列联表，并根据列联表的独立性检验，能否有99%的把握认为以45岁为分界点对“生育二孩放开”政策的支持度有关系？参考数据：

P（K2≥k）	0.050	0.010	0.001
k	3.841	6.635	10.828

${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$

	年龄不低于45岁的人数	年龄低于45岁的人数	合计
支持	3	29	32
不支持	7	11	18
合计	10	40	50

Answer 1

分析 （1）求出样本容量，第二组的频率为0.2，人数为10，即可求出概率；
（2）根据以上统计数据填2×2列联表，求出K²，与临界值比较，即可得出结论．

解答 解：（1）[5，15）年龄段抽取的人数为$\frac{4}{0.8}$=5，频率为0.010×10=0.1，
∴n=$\frac{5}{0.1}$=50，
第二组的频率为0.2，人数为10，则p=$\frac{5}{10}$=0.5；
（2）2×2列联表如下

	年龄不低于45岁的人数	年龄低于45岁的人数	合计
支持	3	29	32
不支持	7	11	18
合计	10	40	50

计算K²=$\frac{50（3×11-7×29）^{2}}{10×40×32×18}$≈6.27＜7.635，
因此没有99%的把握认为以45岁为分界点对“生育二孩放开”政策的支持度有关系．

点评 本题考查了概率的计算，考查了独立性检验的应用问题，是综合性题目．