题目内容
18.在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且$\sqrt{3}a=2csinA$.(1)确定角C的大小;
(2)若$c=\sqrt{7}$,且△ABC的面积为$\frac{{3\sqrt{3}}}{2}$,求△ABC的周长.
分析 (1)由正弦定理化简已知可求$\sqrt{3}sinA=2sinCsinA$,结合范围$0<A<\frac{π}{2}$,求得$sinC=\frac{{\sqrt{3}}}{2}$,结合范围$0<C<\frac{π}{2}$,即可得解C的值.
(2)由已知及三角形面积公式可求ab=6,进而利用余弦定理可求a+b=5,即可得解△ABC的周长.
解答 (本题满分为10分)
解:(1)∵$\sqrt{3}a=2csinA$,由正弦定理得$\sqrt{3}sinA=2sinCsinA$,
又$0<A<\frac{π}{2}$,sinA>0,
∴$sinC=\frac{{\sqrt{3}}}{2}$,
又$0<C<\frac{π}{2}$,
∴$C=\frac{π}{3}$.…(5分)
(2)由已知得$S=\frac{1}{2}absinC=\frac{1}{2}ab×\frac{{\sqrt{3}}}{2}=\frac{{3\sqrt{3}}}{2}$,
∴ab=6…(7分)
在△ABC中,由余弦定理得${a^2}+{b^2}-2abcos\frac{π}{3}=7$,…(8分)
即a2+b2-ab=7,(a+b)2-3ab=7,
又∵ab=6,
∴a+b=5,…(9分)
故△ABC的周长为$a+b+c=5+\sqrt{7}$.…(10分)
点评 本题主要考查了正弦定理,三角形面积公式,余弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知△OAB的直观图△O′A′B′(如图)O′A′=1,∠B′=30°,则△OAB的面积为( )
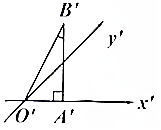

| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$ |
13.已知集合A={1,2,3},B={y|y=x-2,x∈A},则A∩B=( )
| A. | {1} | B. | {4} | C. | {1,3} | D. | {1,4} |
3.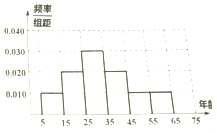 2016年3月31日贵州省第十二届人民代表大会常务委员会第二十一次会议通过的《贵州省人口与计划生育条例》全面开放二孩政策.为了了解人们对于贵州省新颁布的“生育二孩放开”政策的热度,现在某市进行调查,对[5,65]岁的人群随机抽取了n人,得到如下统计表和各年龄段抽取人数频率分布直方图:
2016年3月31日贵州省第十二届人民代表大会常务委员会第二十一次会议通过的《贵州省人口与计划生育条例》全面开放二孩政策.为了了解人们对于贵州省新颁布的“生育二孩放开”政策的热度,现在某市进行调查,对[5,65]岁的人群随机抽取了n人,得到如下统计表和各年龄段抽取人数频率分布直方图:
(1)求n,p的值;
(2)根据以上统计数据填下面2×2列联表,并根据列联表的独立性检验,能否有99%的把握认为以45岁为分界点对“生育二孩放开”政策的支持度有关系?参考数据:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
 2016年3月31日贵州省第十二届人民代表大会常务委员会第二十一次会议通过的《贵州省人口与计划生育条例》全面开放二孩政策.为了了解人们对于贵州省新颁布的“生育二孩放开”政策的热度,现在某市进行调查,对[5,65]岁的人群随机抽取了n人,得到如下统计表和各年龄段抽取人数频率分布直方图:
2016年3月31日贵州省第十二届人民代表大会常务委员会第二十一次会议通过的《贵州省人口与计划生育条例》全面开放二孩政策.为了了解人们对于贵州省新颁布的“生育二孩放开”政策的热度,现在某市进行调查,对[5,65]岁的人群随机抽取了n人,得到如下统计表和各年龄段抽取人数频率分布直方图:| 分组 | 支持“生育二孩”人数 | 占本组的频率 |
| [5,15) | 4 | 0.8 |
| [15,25) | 5 | p |
| [2,35) | 12 | 0.8 |
| [35,45) | 8 | 0.8 |
| [45,55) | 2 | 0.4 |
| [55,65) | 1 | 0.2 |
(2)根据以上统计数据填下面2×2列联表,并根据列联表的独立性检验,能否有99%的把握认为以45岁为分界点对“生育二孩放开”政策的支持度有关系?参考数据:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 支持 | 3 | 29 | 32 |
| 不支持 | 7 | 11 | 18 |
| 合计 | 10 | 40 | 50 |
10.以A(1,3)和B(-5,1)为端点的线段AB的中垂线方程是( )
| A. | 3x-y+8=0 | B. | x-3y+8=0 | C. | 3x+y+8=0 | D. | 3x+y+4=0 |
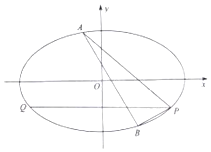 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)