题目内容
10.已知集合P={x∈R|0≤x≤3},Q={x∈R|x2≥4},则P∩(∁RQ)=( )| A. | [0,3] | B. | (0,2] | C. | [0,2) | D. | (0,3] |
分析 化简集合Q,根据交集和补集的定义写出运算结果即可.
解答 解:集合P={x∈R|0≤x≤3},Q={x∈R|x2≥4}={x|x≤-2或x≥2},
则∁RQ={x|-2<x<2},
∴P∩(∁RQ)={x|0≤x<2}=[0,2).
故选:C.
点评 本题考查了集合的化简与运算问题,是基础题目.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
1.方程lnx+2x=6的根所在的区间为( )
| A. | (2,2.25) | B. | (2.25,2.5) | C. | (2.5,2.75) | D. | (2.75,3) |
18.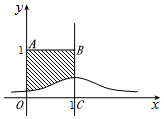 已知随机变量Z~N(1,1),其正态分布密度曲线如图所示,若向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )
已知随机变量Z~N(1,1),其正态分布密度曲线如图所示,若向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )
附:若Z~N(μ,σ2),则 P(μ-σ<Z≤μ+σ)=0.6826;P(μ-2σ<Z≤μ+2σ)=0.9544;P(μ-3σ<Z≤μ+3σ)=0.9974.
 已知随机变量Z~N(1,1),其正态分布密度曲线如图所示,若向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )
已知随机变量Z~N(1,1),其正态分布密度曲线如图所示,若向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )附:若Z~N(μ,σ2),则 P(μ-σ<Z≤μ+σ)=0.6826;P(μ-2σ<Z≤μ+2σ)=0.9544;P(μ-3σ<Z≤μ+3σ)=0.9974.
| A. | 6038 | B. | 6587 | C. | 7028 | D. | 7539 |
15.已知点A是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a,b>0)右支上一点,F是右焦点,若△AOF(O是坐标原点)是等边三角形,则该双曲线离心率e为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
19.若x,y满足约束条件$\left\{{\begin{array}{l}{y≥x}\\{x+y≥1}\\{2x+3y≥3}\end{array}}\right.$则z=3x+4y的最小值为( )
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{21}{5}$ |
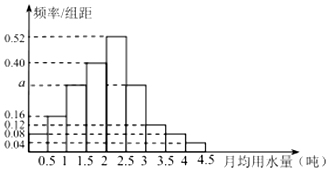 我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过x的部分按平价收费,超过x的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过x的部分按平价收费,超过x的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.