题目内容
5.已知平面向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,且($\overrightarrow{a}$+λ$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$),则实数λ的值为3.分析 计算$\overrightarrow{a}•\overrightarrow{b}$,${\overrightarrow{a}}^{2}$,${\overrightarrow{b}}^{2}$,根据($\overrightarrow{a}$+λ$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$)得出($\overrightarrow{a}$+λ$\overrightarrow{b}$)•(2$\overrightarrow{a}$-$\overrightarrow{b}$)=0,列方程解出λ.
解答 解:∵($\overrightarrow{a}$+λ$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$),
∴($\overrightarrow{a}$+λ$\overrightarrow{b}$)•(2$\overrightarrow{a}$-$\overrightarrow{b}$)=2${\overrightarrow{a}}^{2}$-λ${\overrightarrow{b}}^{2}$+(2λ-1)$\overrightarrow{a}•\overrightarrow{b}$=0,
∵$\overrightarrow{a}•\overrightarrow{b}$=2×1×cos120°=-1,${\overrightarrow{a}}^{2}$=4,${\overrightarrow{b}}^{2}$=1,
∴8-λ+1-2λ=0,解得λ=3.
故答案为:3.
点评 本题考查了平面向量的数量积运算,向量垂直与数量积的关系,属于中档题.

| A. | 30m | B. | 40m | C. | $40\sqrt{3}$m | D. | $40\sqrt{2}$m |
| A. | [0,3] | B. | (0,2] | C. | [0,2) | D. | (0,3] |
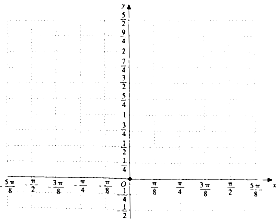 已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.
已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$. 四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )
四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )