题目内容
19.若x,y满足约束条件$\left\{{\begin{array}{l}{y≥x}\\{x+y≥1}\\{2x+3y≥3}\end{array}}\right.$则z=3x+4y的最小值为( )| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{21}{5}$ |
分析 先根据约束条件画出可行域,设z=3x+4y,再利用z的几何意义求最值,只需求出直线z=3x+4y过可行域内的点A时,从而得到z值即可.
解答 解:先根据约束条件$\left\{{\begin{array}{l}{y≥x}\\{x+y≥1}\\{2x+3y≥3}\end{array}}\right.$画出可行域,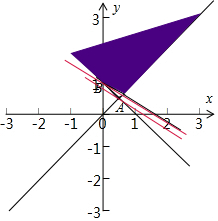
设z=3x+4y,
将最大值转化为y轴上的截距,
当直线z=3x+4y经过点B时,z最大,由$\left\{\begin{array}{l}{x+y=1}\\{2x+3y=3}\end{array}\right.$可得B(0,0)
最大值是:3×0+4×1=4.
故选:C.
点评 本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
9.设集合A={x|x2<2x},B={x|x-1<0},则A∩B=( )
| A. | (-∞,-1) | B. | (-∞,1) | C. | (0,1) | D. | (1,2) |
10.已知集合P={x∈R|0≤x≤3},Q={x∈R|x2≥4},则P∩(∁RQ)=( )
| A. | [0,3] | B. | (0,2] | C. | [0,2) | D. | (0,3] |
8.不等式2x2-x-3>0解集为( )
| A. | {x|-1<x<$\frac{3}{2}$} | B. | {x|x>$\frac{3}{2}$或x<-1} | C. | {x|-$\frac{3}{2}$<x<1} | D. | {x|x>1或x<-$\frac{3}{2}$} |
9.若a∈R,复数z=(a2-2a)+(a2-a-2)i是纯虚数,则( )
| A. | a≠2且a≠-1 | B. | a=0 | C. | a=2 | D. | a=0或a=2 |
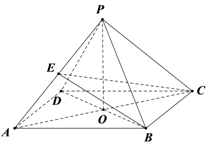 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O