题目内容
11.设函数f(x)=$\left\{\begin{array}{l}{lo{g}_{{2}^{(2-x)}},x<1}\\{1{0}^{x-1}-2,x≥1}\end{array}\right.则f(-6)+f(2)$=11.分析 利用分段函数的性质分别求出f(-6)和f(2),由此能求出f(-6)+f(2)的值.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{{log}_{2}(2-x),x<1}\\{1{0}^{x-1}-2,x≥1}\end{array}\right.$,
∴f(-6)=log28=3,f(2)=102-1-2=8,
∴f(-6)+f(2)=3+8=11.
故答案为:11.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
19.下列各函数中,既是偶函数,又是(0,+∞)上的减函数的是( )
| A. | y=2x | B. | y=-x2 | C. | y=2x | D. | y=log2x |
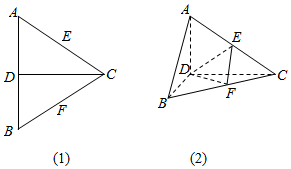 如图(1),正三角形ABC边长为2a,CD是AB边上的高,E,F分别为AC和BC边上的中点,现将△ABC沿CD翻折成直二面角A-DC-B(如图(2))
如图(1),正三角形ABC边长为2a,CD是AB边上的高,E,F分别为AC和BC边上的中点,现将△ABC沿CD翻折成直二面角A-DC-B(如图(2))