题目内容
6.已知直线l的参数方程为$\left\{\begin{array}{l}{x=1+2t}\\{y=\frac{1}{2}-t}\end{array}\right.$,曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ}\end{array}\right.$,设直线l与曲线C交于两点A,B(1)将直线1和曲线C化为普通方程;
(2)若P(1,$\frac{1}{2}$),求|PA|+|PB|,及|PA|•|PB|的值.
分析 (1)根据参数方程解出参数,得出普通方程;
(2)将直线参数方程代入曲线普通方程得出A,B对应的参数值,得出答案.
解答 解:(1)由$\left\{\begin{array}{l}{x=1+2t}\\{y=\frac{1}{2}-t}\end{array}\right.$得x+2y=2,∴直线l的普通方程为x+2y-2=0.
由$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ}\end{array}\right.$得$\left\{\begin{array}{l}{cosθ=\frac{x}{2}}\\{sinθ=y}\end{array}\right.$,∴$\frac{{x}^{2}}{4}+{y}^{2}$=1.∴曲线C的普通方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)将$\left\{\begin{array}{l}{x=1+2t}\\{y=\frac{1}{2}-t}\end{array}\right.$代入$\frac{{x}^{2}}{4}+{y}^{2}$=1得$\frac{(1+2t)^{2}}{4}$+($\frac{1}{2}-t$)2=1,即2t2-$\frac{1}{2}$=0.
∴t=$±\frac{1}{2}$.∴|PA|=|PB|=$\frac{1}{2}$,
∴|PA|+|PB|=$\frac{1}{2}+\frac{1}{2}$=1,|PA|•|PB|=$\frac{1}{4}$.
点评 本题考查了参数方程与普通方程的转化,参数方程的几何意义与应用,属于基础题.

练习册系列答案
相关题目
16.已知不等式mx2+nx-$\frac{1}{m}$<0的解集为{x|x<-$\frac{1}{2}$或x>2},则m-n=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{5}{2}$ | D. | -$\frac{1}{2}$ |
17.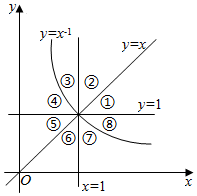 如图,函数$y=\frac{1}{x}$、y=x、y=1的图象和直线x=1将平面直角坐标系的第一象限分成八个部分:①②③④⑤⑥⑦⑧.若幂函数f(x)的图象经过的部分是④⑧,则f(x)可能是( )
如图,函数$y=\frac{1}{x}$、y=x、y=1的图象和直线x=1将平面直角坐标系的第一象限分成八个部分:①②③④⑤⑥⑦⑧.若幂函数f(x)的图象经过的部分是④⑧,则f(x)可能是( )
 如图,函数$y=\frac{1}{x}$、y=x、y=1的图象和直线x=1将平面直角坐标系的第一象限分成八个部分:①②③④⑤⑥⑦⑧.若幂函数f(x)的图象经过的部分是④⑧,则f(x)可能是( )
如图,函数$y=\frac{1}{x}$、y=x、y=1的图象和直线x=1将平面直角坐标系的第一象限分成八个部分:①②③④⑤⑥⑦⑧.若幂函数f(x)的图象经过的部分是④⑧,则f(x)可能是( )| A. | y=x2 | B. | $y=\frac{1}{{\sqrt{x}}}$ | C. | $y={x^{\frac{1}{2}}}$ | D. | y=x-2 |