Question

如图，平面ABEF⊥平面ABC，四边形ABEF为矩形，AC=BC．O为AB的中点，OF⊥EC．
（Ⅰ）求证：OE⊥FC；
（Ⅱ）若二面角F-CE-B的余弦值为-

1

3

时，求

AC

AB

的值．

Answer 1

考点：与二面角有关的立体几何综合题

专题：综合题,空间位置关系与距离

分析：（Ⅰ）连结OC，则OC⊥AB，从而得到OC⊥OF，进而得到OF⊥OE，由此能证明OE⊥FC．
（Ⅱ）由（I）得AB=2AF．不妨设AF=1，AB=2，取EF的中点为O，建立坐标系，求出平面FCE的法向量、平面CEB的法向量，利用向量的夹角公式，结合若二面角F-CE-B的余弦值为-

1

3

，求出k的值，即可求

AC

AB

的值．

解答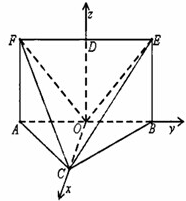： （Ⅰ）证明：连结OC，∵AC=BC，O是AB的中点，
故OC⊥AB．  
又∵平面ABC⊥平面ABEF，
故OC⊥平面ABE，于是OC⊥OF．
又OF⊥EC，∵OF⊥平面OEC，
∴OF⊥OE，
又∵OC⊥OE，∴OE⊥平面OFC，
∴OE⊥FC；
（Ⅱ）解：由（I）得AB=2AF．不妨设AF=1，AB=2，取EF的中点为O，建立坐标系，设OC=k，
则F（0，-1，1），E（0，1，1），B（0，1，0），C（k，0，0），则

CE

=（-k，1，1），

EF

=（0，-2，0），
设平面FCE的法向量为

m

=（x，y，z），
则

-kx+y+z=0 -2y=0

．
∴

m

=（1，0，k），
∵

BE

=（0，0，1），

BC

=（k，-1，0），
∴同理可得平面CEB的法向量为

n

=（1，k，0），
∴cos＜

m

，

n

＞=

1

k2+1

=

1

3

，
∴k=

2

，
∴AC=

k2+1

=

3

，
∴

AC

AB

=

3

2

．

点评：本题考查异面直线垂直的证明，考查二面角的余弦值的求法，考查向量方法的运用，解题时要认真审题，注意空间思维能力的培养．