��Ŀ����
17���ڶ����ǵ����з�ʽ��һ�ε����У������� ��100�ˣ�����Ů��55�ˣ�����45�ˣ�Ů������40����Ҫ�����з�ʽ�ǿ����ӣ�����15����Ҫ�����з�ʽ���˶�����������20����Ҫ���з�ʽ�ǿ����ӣ�����25����Ҫ���з�ʽ���˶�����1�������������ݽ���һ��2��2����������
��2���Ƿ���99%�İ�����Ϊ�Ա������з�ʽ�й�ϵ��${K^2}=\frac{{n{{��ad-bc��}^2}}}{��a+b����c+d����a+c����b+d��}$
| p��k2��k0�� | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
���� ��1�����������������������
��2������K2�Ĺ۲�ֵ�������ٽ�ֵ���ɵó����ۣ�
��� �⣺��1�������������ݵõ���������
| ���з�ʽ �Ա� | ������ | �˶� | �ϼ� |
| Ů | 43 | 27 | 70 |
| �� | 21 | 33 | 54 |
| �ϼ� | 64 | 60 | 124 |
$\frac{124{����43��33-27��21��}^{2}}{70��54��64��60}$��6.201��6.635��
��P��K2��6.635��=0.01��
��û��99%�İ�����Ϊ�Ա������з�ʽ�й�ϵ��
���� ���⿼���˶����Լ����Ӧ�����⣬�ǻ����⣮

��ϰ��ϵ�д�
�����Ŀ
19��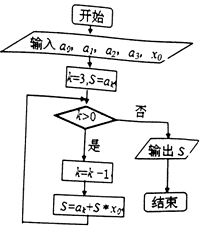 �ؾ������ҹ�����ʱ������ѧ�ң����������������¡����ҹ�13������ѧ�ɾ͵Ĵ���֮һ����ͼ���ؾ����㷨��һ�������ͼ���������SΪ��������
�ؾ������ҹ�����ʱ������ѧ�ң����������������¡����ҹ�13������ѧ�ɾ͵Ĵ���֮һ����ͼ���ؾ����㷨��һ�������ͼ���������SΪ��������
 �ؾ������ҹ�����ʱ������ѧ�ң����������������¡����ҹ�13������ѧ�ɾ͵Ĵ���֮һ����ͼ���ؾ����㷨��һ�������ͼ���������SΪ��������
�ؾ������ҹ�����ʱ������ѧ�ң����������������¡����ҹ�13������ѧ�ɾ͵Ĵ���֮һ����ͼ���ؾ����㷨��һ�������ͼ���������SΪ��������| A�� | a1+x0��a3+x0��a0+a2x0������ֵ | B�� | a3+x0��a2+x0��a1+a0x0������ֵ | ||
| C�� | a0+x0��a1+x0��a2+a3x0������ֵ | D�� | a2+x0��a0+x0��a3+a1x0������ֵ |
8����֪����f��x��=$\frac{4}{3}$x3-2kx2-x+1��������ͬ�ļ�ֵ��x1��x2��x1��1��x2������g��x��=$\frac{2x-k}{{x}^{2}+1}$����x��[1��x2]ʱ��g��x����$\frac{k}{2}$���������ʵ��k��ȡֵ��Χ�ǣ�������
| A�� | ��$\frac{3}{4}$��+�ޣ� | B�� | [1��+�ޣ� | C�� | ��$\frac{3}{4}$��1] | D�� | {1} |
2����֪����p��1��{x|x2-2x+1��0}������q��?x��[0��1]��x2-1��0����������������������ǣ�������
| A�� | p��q | B�� | �Vp�ģ��Vq�� | C�� | p��q | D�� | �Vp��q |
13����������$\left\{\begin{array}{l}{x=t}\\{y=1+t}\end{array}\right.$��tΪ��������ʾ�����ǣ�������
| A�� | һ������ | B�� | �������� | C�� | һ��ֱ�� | D�� | ����ֱ�� |
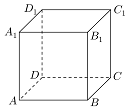 ��ͼ��ABCD-A1B1C1D1���ⳤΪ1�������壬����ƽ�����Խ���AC1��ֱ��ʹ�æ����������ÿ���涼�й����㣬�����õ��Ľ������ε����ΪS���ܳ�Ϊl�ķ�Χ�ֱ���[$\frac{\sqrt{3}}{2}$��$\frac{3\sqrt{3}}{4}$]��{3$\sqrt{2}$}���ü��ϱ�ʾ��
��ͼ��ABCD-A1B1C1D1���ⳤΪ1�������壬����ƽ�����Խ���AC1��ֱ��ʹ�æ����������ÿ���涼�й����㣬�����õ��Ľ������ε����ΪS���ܳ�Ϊl�ķ�Χ�ֱ���[$\frac{\sqrt{3}}{2}$��$\frac{3\sqrt{3}}{4}$]��{3$\sqrt{2}$}���ü��ϱ�ʾ��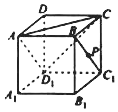 ��������ABCD-A1B1C1D1�У���ͼ������֪��P��ֱ��BC1���˶����������ĸ����⣺
��������ABCD-A1B1C1D1�У���ͼ������֪��P��ֱ��BC1���˶����������ĸ����⣺