题目内容
15.已知函数f(x)是定义在(-∞,+∞)上的偶函数,且在[0,+∞)上是增函数,若实数a满足:$f({log_3}a)+f({log_3}\frac{1}{a})≤2f(1)$,则a的取值范围是$\frac{1}{3}$≤a≤3.分析 由于函数f(x)是定义在R上的偶函数,则f(-x)=f(x),即有f(x)=f(|x|),$f({log_3}a)+f({log_3}\frac{1}{a})≤2f(1)$,即为f(|log3a|)≤f(1),再由f(x)在区间[0,+∞)上单调递增,得到|log3a|≤1,即有-1≤log3a≤1,解出即可
解答 解:由于函数f(x)是定义在R上的偶函数,
则f(-x)=f(x),即有f(x)=f(|x|),
由实数a满足$f({log_3}a)+f({log_3}\frac{1}{a})≤2f(1)$,
则有f(log3a)+f(-log3a)≤2f(1),
即2f(log3a)≤2f(1)即f(log3a)≤f(1),
即有f(|log3a|)≤f(1),
由于f(x)在区间[0,+∞)上单调递增,
则|log3a|≤1,即有-1≤log3a≤1,
解得,$\frac{1}{3}$≤a≤3.
故答案为:$\frac{1}{3}$≤a≤3.
点评 本题考查函数的性质和运用,考查函数的奇偶性、单调性和运用,考查对数不等式的解法,考查运算能力,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若复数z满足$i•z=-\frac{1}{2}(1+i)$,则z的共轭复数的虚部是( )
| A. | $-\frac{1}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
 中,
中, ,
, ,
, 为
为 的中点,
的中点, ,则
,则 的长为_________.
的长为_________.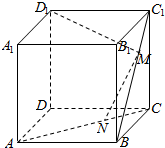 如图,正方体ABCD-A1B1C1D1的棱长为a,$\frac{AN}{NC}=\frac{BM}{{M{C_1}}}=3$.
如图,正方体ABCD-A1B1C1D1的棱长为a,$\frac{AN}{NC}=\frac{BM}{{M{C_1}}}=3$.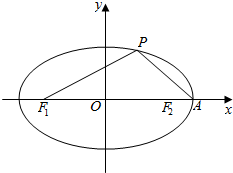 如图,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左、右两个焦点分别为F1、F2,A为椭圆的右顶点,点P在椭圆上且∠PF1F2=arccos$\frac{7}{8}$
如图,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左、右两个焦点分别为F1、F2,A为椭圆的右顶点,点P在椭圆上且∠PF1F2=arccos$\frac{7}{8}$