题目内容
如图,已知曲线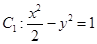 ,曲线
,曲线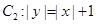 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与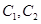 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.
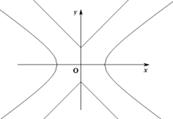
(1)在正确证明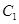 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线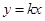 与
与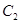 有公共点,求证
有公共点,求证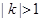 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆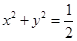 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
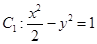 ,曲线
,曲线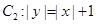 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与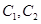 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.
(1)在正确证明
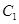 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);(2)设直线
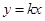 与
与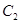 有公共点,求证
有公共点,求证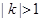 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;(3)求证:圆
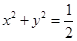 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”. (1) C1的左焦点为“C1-C2型点”,且直线可以为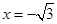 ;
;
(2)直线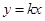 至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
(3)直线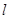 若与圆
若与圆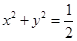 内有交点,则不可能同时与曲线C1和C2有交点,
内有交点,则不可能同时与曲线C1和C2有交点,
即圆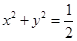 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.
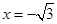 ;
; (2)直线
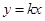 至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”. (3)直线
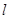 若与圆
若与圆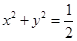 内有交点,则不可能同时与曲线C1和C2有交点,
内有交点,则不可能同时与曲线C1和C2有交点, 即圆
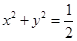 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.试题分析:
思路分析:(1)紧扣“C1-C2型点”的定义,确定C1的左焦点为“C1-C2型点”,且直线可以为
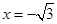 ;
; (2)通过研究直线
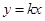 与C2有交点的条件,分别得到
与C2有交点的条件,分别得到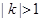 和
和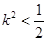 ,不可能同时成立,得到结论:直线
,不可能同时成立,得到结论:直线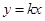 至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”. (3)显然过圆
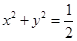 内一点的直线
内一点的直线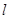 若与曲线C1有交点,则斜率必存在;
若与曲线C1有交点,则斜率必存在; 根据对称性,不妨设直线
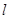 斜率存在且与曲线C2交于点
斜率存在且与曲线C2交于点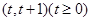 ,则
,则 
根据直线
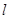 与圆
与圆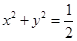 内部有交点,得到
内部有交点,得到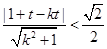
化简得,
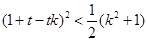 ............①
............①再根据直线
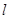 与曲线C1有交点, 由方程组
与曲线C1有交点, 由方程组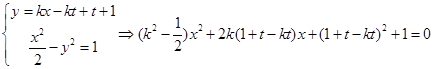
化简得,
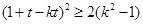 .....②
.....②由①②得,
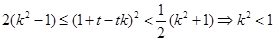
但此时,因为
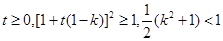 ,即①式不成立;
,即①式不成立; 当
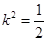 时,①式也不成立 ,得出结论。
时,①式也不成立 ,得出结论。解:(1)C1的左焦点为
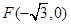 ,过F的直线
,过F的直线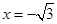 与C1交于
与C1交于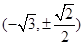 ,与C2交于
,与C2交于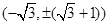 ,故C1的左焦点为“C1-C2型点”,且直线可以为
,故C1的左焦点为“C1-C2型点”,且直线可以为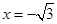 ;
; (2)直线
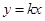 与C2有交点,
与C2有交点,则
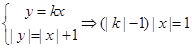 ,若方程组有解,则必须
,若方程组有解,则必须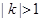 ;
; 直线
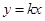 与C2有交点,则
与C2有交点,则 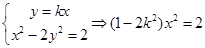 ,若方程组有解,则必须
,若方程组有解,则必须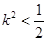
故直线
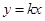 至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”. (3)显然过圆
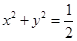 内一点的直线
内一点的直线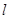 若与曲线C1有交点,则斜率必存在;
若与曲线C1有交点,则斜率必存在; 根据对称性,不妨设直线
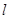 斜率存在且与曲线C2交于点
斜率存在且与曲线C2交于点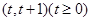 ,则
,则 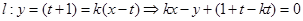
直线
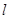 与圆
与圆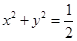 内部有交点,故
内部有交点,故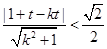
化简得,
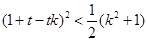 ............①
............①若直线
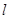 与曲线C1有交点,则
与曲线C1有交点,则 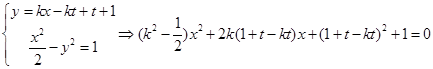

化简得,
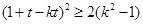 .....②
.....②由①②得,
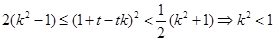
但此时,因为
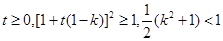 ,即①式不成立;
,即①式不成立; 当
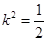 时,①式也不成立
时,①式也不成立 综上,直线
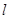 若与圆
若与圆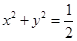 内有交点,则不可能同时与曲线C1和C2有交点,
内有交点,则不可能同时与曲线C1和C2有交点, 即圆
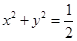 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.点评:难题,本题综合性较强,综合考查直线与圆、双曲线的位置关系以及不等式问题。从思路方面讲,要紧扣“C1-C2型点”的定义,研究方程组解的情况。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
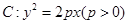 的焦点为
的焦点为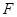 ,准线为
,准线为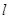 ,
,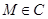 ,以
,以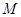 为圆心的圆
为圆心的圆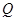 ,
,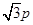 ,
,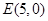 是圆
是圆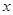 轴除
轴除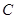 与圆
与圆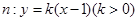 ,
,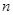 与
与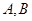 两点,
两点,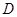 ,且
,且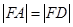 , 求
, 求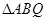 的面积.
的面积.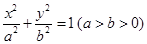 的左右顶点分别为
的左右顶点分别为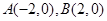 ,离心率
,离心率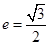 .过该椭圆上任一点
.过该椭圆上任一点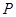 作
作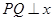 轴,垂足为
轴,垂足为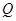 ,点
,点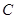 在
在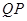 的延长线上,且
的延长线上,且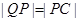 .
.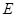 的方程;
的方程;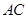 (
(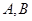 )与直线
)与直线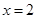 交于点
交于点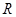 ,
,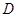 为线段
为线段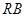 的中点,试判断直线
的中点,试判断直线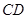 与曲线
与曲线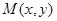 与定点
与定点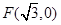 的距离和它到直线
的距离和它到直线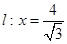 的距离之比是常数
的距离之比是常数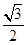 ,记
,记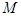 的轨迹为曲线
的轨迹为曲线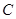 .
.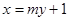 与曲线
与曲线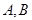 两点,点
两点,点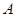 关于
关于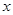 轴的对称点为
轴的对称点为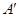 ,试问:当
,试问:当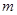 变化时,直线
变化时,直线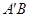 与
与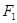 、
、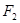 为双曲线
为双曲线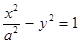 的两个焦点,点
的两个焦点,点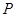 在此双曲线上,
在此双曲线上,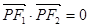 ,如果此双曲线的离心率等于
,如果此双曲线的离心率等于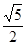 ,那么点
,那么点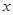 轴的距离等于 .
轴的距离等于 .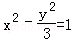 的渐近线的距离是( )
的渐近线的距离是( )
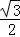
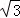
 中,已知
中,已知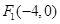 ,直线
,直线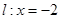 , 动点
, 动点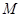 到
到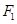 的距离是它到定直线
的距离是它到定直线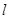 距离的
距离的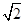 倍. 设动点
倍. 设动点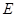 .
. 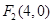 , 若直线
, 若直线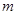 为曲线
为曲线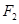 到
到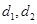 ,试判断
,试判断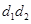 是否为常数,请说明理由.
是否为常数,请说明理由. 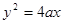 (
(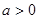 且
且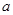 为常数),
为常数),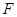 为其焦点.
为其焦点.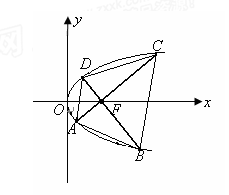
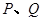 两点,且
两点,且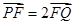 ,求直线
,求直线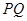 的斜率;
的斜率;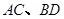 是过抛物线焦点
是过抛物线焦点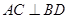 ,如图所示.求四边形
,如图所示.求四边形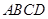 面积的最小值
面积的最小值 .
.