题目内容
已知抛物线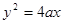 (
(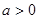 且
且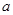 为常数),
为常数),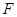 为其焦点.
为其焦点.
(1)写出焦点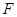 的坐标;
的坐标;
(2)过点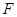 的直线与抛物线相交于
的直线与抛物线相交于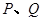 两点,且
两点,且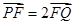 ,求直线
,求直线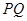 的斜率;
的斜率;
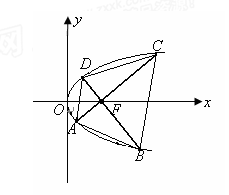
(3)若线段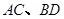 是过抛物线焦点
是过抛物线焦点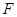 的两条动弦,且满足
的两条动弦,且满足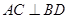 ,如图所示.求四边形
,如图所示.求四边形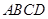 面积的最小值
面积的最小值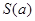 .
.
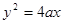 (
(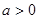 且
且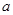 为常数),
为常数),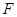 为其焦点.
为其焦点.
(1)写出焦点
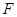 的坐标;
的坐标;(2)过点
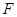 的直线与抛物线相交于
的直线与抛物线相交于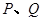 两点,且
两点,且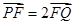 ,求直线
,求直线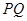 的斜率;
的斜率;(3)若线段
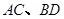 是过抛物线焦点
是过抛物线焦点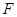 的两条动弦,且满足
的两条动弦,且满足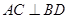 ,如图所示.求四边形
,如图所示.求四边形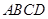 面积的最小值
面积的最小值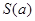 .
.(1)(a,0);(2) ; (3)
; (3)  .
.
 ; (3)
; (3)  .
.试题分析:(1)∵抛物线方程为
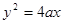 (a>0),∴焦点为F(a,0).
(a>0),∴焦点为F(a,0).(2)设满足题意的点为P(x0,y0)、Q(x1,y1).
∵
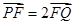 ,
,∴(a-x0,-y0)=2(x1-a,y1),即
 .
.又y12=4ax1,y02=4ax0,
∴
 ,进而可得x0=2a,
,进而可得x0=2a, ,即y0=±2
,即y0=±2 a.
a.∴
 .
.(3) 由题意可知,直线AC不平行于x轴、y轴(否则,直线AC、BD与抛物线不会有四个交点)。
于是,设直线AC的斜率为
 . 12分
. 12分联立方程组
 ,化简得
,化简得 (设点
(设点 ),则
),则 是此方程的两个根.
是此方程的两个根. . 13分
. 13分弦长

=

=

=
 . 15分
. 15分又
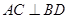 ,
, .
. . 16分
. 16分
=
 ,当且仅当
,当且仅当 时,四边形
时,四边形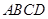 面积的最小值
面积的最小值 .18分
.18分点评:中档题,涉及曲线的位置关系问题,往往通过联立方程组,消元后,应用韦达定理,简化运算过程。本题(2)通过应用平面向量共线的条件,利用“代入法”,得到
 的关系,进一步求得直线的斜率。(3)利用函数的观点及均值定理,确定得到面积的最小值。应用均值定理要注意“一正,二定,三相等”,缺一不可。
的关系,进一步求得直线的斜率。(3)利用函数的观点及均值定理,确定得到面积的最小值。应用均值定理要注意“一正,二定,三相等”,缺一不可。
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为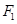 、
、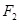 ,离心率为3,直线y=2与C的两个交点间的距离为
,离心率为3,直线y=2与C的两个交点间的距离为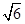 .
.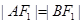 ,证明:
,证明: 、
、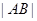 、
、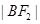 成等比数列.
成等比数列.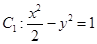 ,曲线
,曲线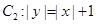 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与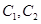 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.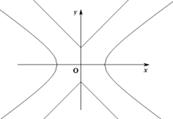
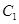 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);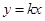 与
与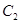 有公共点,求证
有公共点,求证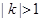 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;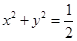 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”. ( )
( )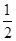
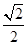
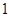
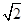
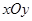 中,直线
中,直线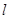 的方程为
的方程为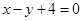 ,曲线
,曲线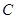 的参数方程为
的参数方程为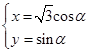 (
(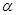 为参数).
为参数).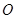 为极点,以
为极点,以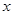 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点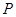 的极坐标为(4,
的极坐标为(4,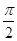 ),判断点
),判断点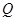 是曲线
是曲线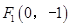 、
、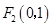 且过点
且过点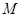
 椭圆;
椭圆; 有相同的渐近线,且过点
有相同的渐近线,且过点 的双曲线.
的双曲线.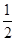 ,短轴长为4
,短轴长为4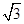 .
.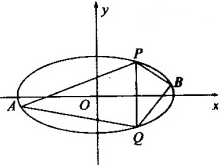
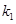 ,直线PB的斜率为
,直线PB的斜率为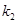 ,判断
,判断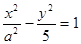 的右焦点为(3,0),则该双曲线的离心率等于 ( )
的右焦点为(3,0),则该双曲线的离心率等于 ( )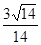

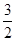 .
.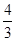
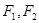 分别是椭圆
分别是椭圆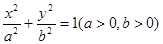 的左右焦点,过
的左右焦点,过 与
与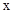 轴垂直的直线交椭圆于
轴垂直的直线交椭圆于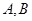 两点,若
两点,若 是锐角三角形,则椭圆离心率的范围是( )
是锐角三角形,则椭圆离心率的范围是( )