题目内容
定义两个实数间的一种新运算“*”:x*y=ln(ex+ey),x,y∈R.当x*x=y时,x=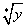 .对任意实数a,b,c,给出如下命题:
.对任意实数a,b,c,给出如下命题:
①a*b=b*a;
②(a*b)+c=(a+c)*(b+c);
③(a*b)-c=(a-c)*(b-c);
④(a*b)*c=a*(b*c);
⑤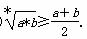
其中正确的命题有________.(写出所有正确的命题序号)
①②③④⑤
解析 因为a*b=ln(ea+eb),b*a=ln(eb+ea),
所以a*b=b*a,即①对;
因为(a*b)+c=ln(ea+eb)+c=ln[(ea+eb)ec]
=ln(ea+c+eb+c)=(a+c)*(b+c),所以②对;
只需令②中的c为-c,即有结论(a*b)-c=(a-c)*(b-c),所以③对;
因为(a*b)*c=[ln(ea+eb)]*c=ln[ +ec]
+ec]
=ln(ea+eb+ec),
a*(b*c)=a*[ln(eb+ec)]=ln[ea+ ]
]
=ln(ea+eb+ec),
所以(a*b)*c=a*(b*c),即④对;
设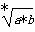 =x,则x*x=a*b,
=x,则x*x=a*b,
所以ln(ex+ex)=ln(ea+eb),
所以2×ex=ea+eb,
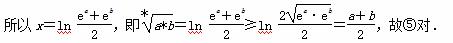 故正确的命题是①②③④⑤.
故正确的命题是①②③④⑤.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线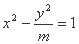 与抛物线
与抛物线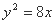 的一个交点为
的一个交点为 ,
,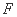 为抛物线的焦点,若
为抛物线的焦点,若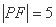 ,则双曲线的渐近线方程为 ( )
,则双曲线的渐近线方程为 ( )
| (A) | (B) | (C) | (D) |
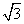 asin xcos x+a+b(a≠0)的定义域是
asin xcos x+a+b(a≠0)的定义域是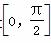 ,值域是[-5,1],求常数a,b的值.
,值域是[-5,1],求常数a,b的值. ,
, 共线的充要条件是
共线的充要条件是 ,
,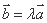 D.存在不全为零的实数
D.存在不全为零的实数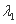 ,
, ,
,
 与
与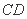 相交于点
相交于点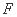 ,
,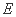 是
是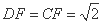 ,
, ∶
∶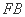 ∶
∶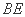
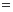
 ∶
∶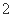 ∶
∶ . 若
. 若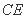 与该圆
与该圆 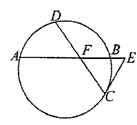
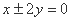
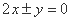
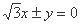
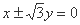
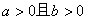 ”,条件乙:“方程
”,条件乙:“方程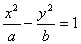 表示双曲线”,那么甲是乙的( )
表示双曲线”,那么甲是乙的( )