题目内容
15.设函数f(x)=$\frac{1}{3}$x3+mx2+1的导函数f′(x),且f′(1)=3.(1)求函数f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调区间和极值.
分析 (1)求出f′(x)=x2+2mx,利用f′(1)=3.求出m,求出切线斜率,切点坐标,得到切线方程.
(2)利用导函数的符号,求解函数f(x)的单调递增区间,递减区间即可.
解答 解:(1)f′(x)=x2+2mx,f′(1)=3,
∴f′(x)=1+2m=3,∴m=1.
∴f(x)=$\frac{1}{3}$x3+x2+1,∴f(1)=$\frac{7}{3}$.
∴切线方程为y-$\frac{7}{3}$=3(x-1),
即3x-3y+4=0.
(2)f′(x)=x2+2x=x(x+2),
令f′(x)>0,得x>0或x<-2,
令f′(x)<0,得-2<x<0,
∴函数f(x)的单调递增区间为(-∞,-2),(0,+∞),递减区间为(-2,0).
点评 本题考查函数的导数的应用,切线方程以及函数的单调区间的求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.复平面上三点A、B、C分别对应复数1,2i,5+2i,则由A,B,C为顶点所构成的三角形是( )
| A. | 锐角三角形 | B. | 等腰三角形 | C. | 钝角三角形 | D. | 直角三角形 |
3.某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则三棱锥的体积为( )
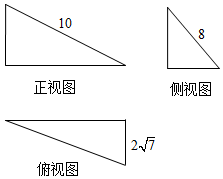

| A. | 32 | B. | $32\sqrt{7}$ | C. | $16\sqrt{7}$ | D. | $64\sqrt{7}$ |
2.一个盒子中共有12个大小相同的小球,其中红球9个,黄球3个,从盒子中任取3个球,将其中的红球染成黄色连同黄球一起放回,此时盒子中黄球的个数为ξ,则Eξ=( )
| A. | 1 | B. | $\frac{21}{4}$ | C. | $\frac{17}{4}$ | D. | 3 |
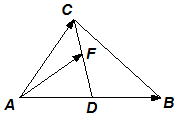 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.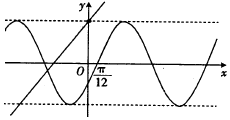 已知函数y=ksin(kx+φ)(|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则φ=-$\frac{π}{6}$.
已知函数y=ksin(kx+φ)(|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则φ=-$\frac{π}{6}$.