题目内容
设b和c分别是先后抛掷一枚骰子得到的点数,则方程x2+bx+c=0有实根的概率为 .
考点:几何概型
专题:概率与统计
分析:本题是一个等可能事件的概率,试验发生包含的事件数是6×6=36种结果,方程x2+bx+c=0有实根要满足判别式不小于0,列举出结果.
解答:
解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件数是6×6=36种结果,
方程x2+bx+c=0有实根要满足b2-4c≥0,
当b=2,c=1
b=3,c=1,2
b=4,c=1,2,3,4
b=5,c=1,2,3,4,5,6,
b=6,c=1,2,3,4,5,6
综上可知共有1+2+4+6+6=19种结果
∴方程x2+bx+c=0有实根的概率是
;
故答案为:
.
试验发生包含的事件数是6×6=36种结果,
方程x2+bx+c=0有实根要满足b2-4c≥0,
当b=2,c=1
b=3,c=1,2
b=4,c=1,2,3,4
b=5,c=1,2,3,4,5,6,
b=6,c=1,2,3,4,5,6
综上可知共有1+2+4+6+6=19种结果
∴方程x2+bx+c=0有实根的概率是
| 19 |
| 36 |
故答案为:
| 19 |
| 36 |
点评:本题考查古典概型的等可能事件的概率,在解题过程中主要应用列举法来列举出所有的满足条件的事件数.

练习册系列答案
相关题目
已知椭圆
+
=1与双曲线12y2-4x2=3,F1,F2是它们的焦点,M是它们的一个交点,则△MF1F2是( )
| x2 |
| 3 |
| y2 |
| 4 |
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、等边三角形 |
 已知四棱锥P-ABCD,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形,E是侧棱PC上的 一点,点F在线段BD上,且满足DF=3BF,若EF∥平面PAB.
已知四棱锥P-ABCD,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形,E是侧棱PC上的 一点,点F在线段BD上,且满足DF=3BF,若EF∥平面PAB.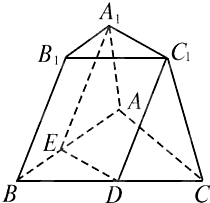 如图所示,在两个底面对应边的比是1:2的三棱台ABC-A1B1C1中,BB1∥截面A1EDC1,求截面A1EDC1截棱台ABC-A1B1C1成两部分体积之比.
如图所示,在两个底面对应边的比是1:2的三棱台ABC-A1B1C1中,BB1∥截面A1EDC1,求截面A1EDC1截棱台ABC-A1B1C1成两部分体积之比.