题目内容
(1)解含x的不等式:22x+1<(
)2-3x;
(2)求函数y=log2(x2-2x+3)的值域,并写出其单调区间.
| 1 |
| 4 |
(2)求函数y=log2(x2-2x+3)的值域,并写出其单调区间.
考点:指、对数不等式的解法,对数函数的图像与性质
专题:函数的性质及应用,不等式的解法及应用
分析:(1)利用指数函数的单调性化简不等式,求解即可.
(2)通过二次函数的对称轴,以及对数函数的单调性,通过复合函数的单调性写出单调区间即可.
(2)通过二次函数的对称轴,以及对数函数的单调性,通过复合函数的单调性写出单调区间即可.
解答:
解:(1):22x+1<(
)2-3x=26x-4,
∵y=2x,是增函数,
∴2x+1<6x-4,
∴x>
…(4分)
(2)函数y=log2(x2-2x+3),x2-2x+3=(x-1)2+2≥2,x∈[1,+∞)时,x2-2x+3是增函数,
数y=log2x是增函数,由防晒霜的单调性可知:函数y=log2(x2-2x+3),
满足y∈[1,+∞)…(6分)
函数y=log2(x2-2x+3)的增区间[1,+∞),减区间(-∞,1]…(8分).
| 1 |
| 4 |
∵y=2x,是增函数,
∴2x+1<6x-4,
∴x>
| 5 |
| 4 |
(2)函数y=log2(x2-2x+3),x2-2x+3=(x-1)2+2≥2,x∈[1,+∞)时,x2-2x+3是增函数,
数y=log2x是增函数,由防晒霜的单调性可知:函数y=log2(x2-2x+3),
满足y∈[1,+∞)…(6分)
函数y=log2(x2-2x+3)的增区间[1,+∞),减区间(-∞,1]…(8分).
点评:本题考查指数函数的单调性以及对数函数的单调性的应用,指数对数不等式的解法,考查计算能力.

练习册系列答案
相关题目
下列函数在区间(0,+∞)上为增函数的是( )
| A、y=1-2x | ||
| B、y=x2+2x | ||
| C、y=-x2 | ||
D、y=
|
若数列的前4项分别是
,-
,
,-
,则此数列的一个通项公式为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
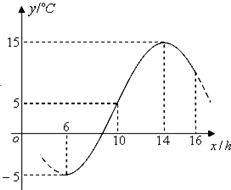 如图,某地一天6-16时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,其中A>0,ω>0,0<φ<π.
如图,某地一天6-16时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,其中A>0,ω>0,0<φ<π.