题目内容
11.设函数f(x)是定义在R上的奇函数,当x∈(0,+∞)时,f(x)=x2-2x+2.(1)求f(x)在R上的解析式;
(2)设g(x)=f(2x)+2m-1(m∈R),若对任意x∈R,都有g(x)≥0恒成立,求实数m的取值范围.
分析 (1)可设x<0,从而有-x>0,这便可得到f(-x)=x2+2x+2=-f(x),这便可得到x<0时f(x)的解析式,而f(0)=0,从而便可写出f(x)在R上的解析式;
(2)2x>0,从而可得到g(x)=(2x)2-2•2x+2m+1≥0恒成立,可设2x=t,t>0,这便可得到m$≥-\frac{{t}^{2}}{2}+t-\frac{1}{2}$,t>0,恒成立,而$-\frac{{t}^{2}}{2}+t-\frac{1}{2}=-\frac{1}{2}(t-1)^{2}≤0$,从而有m≥0,这便得出了实数m的取值范围.
解答 解:(1)设x<0,-x>0,则:
f(-x)=x2+2x+2=-f(x);
∴f(x)=-x2-2x-2;
又f(x)为R上的奇函数,∴f(0)=0;
∴$f(x)=\left\{\begin{array}{l}-{x^2}-2x-2,(x<0)\\ 0,(x=0)\\{x^2}-2x+2,(x>0)\end{array}\right.$;
(2)由题意g(x)=(2x)2-2•2x+2m+1≥0恒成立,设2x=t,t>0;
∴t2-2t+2m+1≥0恒成立;
∴$m≥-\frac{t^2}{2}+t-\frac{1}{2}(t>0)$恒成立,而$y=-\frac{t^2}{2}+t-\frac{1}{2}=-\frac{1}{2}{(t-1)^2}≤0$;
∴m≥0;
∴实数m的取值范围为[0,+∞).
点评 考查奇函数的定义,对于奇函数,已知一区间上的解析式,求其对称区间上解析式的方法,奇函数在原点有定义时,原点处的函数值为0,以及指数函数的值域,配方求二次函数范围的方法.

练习册系列答案
相关题目
3.已知集合M={x|$\frac{2}{x}$≥1},N={y|y=1-x2},则M∩N=( )
| A. | (-∞,2] | B. | (0,1] | C. | (0,2] | D. | [0,1] |
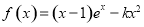 (其中
(其中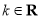 ).
).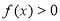 对
对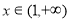 恒成立,求实数
恒成立,求实数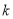 的取值范围;
的取值范围;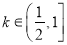 时,求函数
时,求函数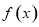 在
在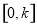 上的最大值
上的最大值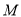 .
.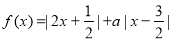 .
.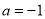 时,解不等式
时,解不等式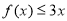 ;
;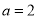 时,若关于
时,若关于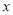 的不等式
的不等式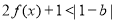 的解集为空集,求实数
的解集为空集,求实数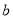 的取值范围.
的取值范围.