题目内容
19.如果一个水平放置的图形的斜二测直观图是一个底角均为45°,腰和上底均为1的等腰梯形,那么原平面图形的周长为4+$\sqrt{2}$+$\sqrt{6}$.分析 利用原图和直观图的关系,可得直观图,利用梯形周长公式求解即可.
解答 解:恢复后的原图形为一直角梯形,上底为1,高为2,下底为1+$\sqrt{2}$,
另一腰长为:$\sqrt{(1+\sqrt{2}-1)^{2}+{2}^{2}}$=$\sqrt{6}$,
故原图的周长为:1+2+1+$\sqrt{2}$+$\sqrt{6}$=4+$\sqrt{2}$+$\sqrt{6}$,
故答案为:4+$\sqrt{2}$+$\sqrt{6}$
点评 本题考查水平放置的平面图形的直观图斜二测画法,属基础知识的考查.

练习册系列答案
相关题目
8.不等式|x-3|<2的解集是( )
| A. | {x|x>5或x<1} | B. | {x|1<x<5} | C. | {x|-5<x<-1} | D. | {x|x>1} |
4.计算log92•log827=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
8.已知x=lnπ,$y={log_5}\frac{2}{3}$,$z={e^{-\frac{1}{2}}}$,则( )
| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
7.设不等式组$\left\{\begin{array}{l}{x-y+4≤0}\\{x+y-2≤0}\\{y-2≥0}\\{\;}\end{array}\right.$示的平面区域为D.若指数函数y=ax(a>0且a≠1)的图象经过区域D上的点,则a的取值范围是( )
| A. | [$\sqrt{2}$,3] | B. | [3,+∞) | C. | (0,$\frac{1}{3}$] | D. | [$\frac{1}{3}$,1) |
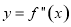 是
是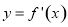 的导数.某同学经过探究发现,任意一个三次函数
的导数.某同学经过探究发现,任意一个三次函数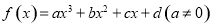 都有对称中心
都有对称中心 ,其中
,其中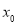 满足
满足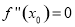 .已知函数
.已知函数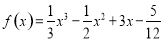 ,则
,则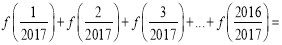 ( )
( )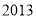 B.
B. C.
C. D.
D.
 的值为( )
的值为( ) B.
B. C.
C. D.
D.