题目内容
3.对于数列{an},若an+2-an=d(d是与n无关的常数,n∈N*),则称数列{an}叫做“弱等差数列”,已知数列{an}满足:a1=t,a2=s且an+an+1=an+b对于n∈N*恒成立,(其中t,s,a,b都是常数).(1)求证:数列{an}是“弱等差数列”,并求出数列{an}的通项公式;
(2)当t=1,s=3时,若数列{an}是等差数列,求出a、b的值,并求出{an}的前n项和Sn;
(3)若s>t,且数列{an}是单调递增数列,求a的取值范围.
分析 (1)由已知得an+2=a(n+1)+b-an+1=(an+a+b)-(an+b)+an=a+an,由此能证明数列{an}是“弱等差数列”.由a1=t,a2=s,an+2-an=a,得到{an}中奇数项是以t为首项,以a为公差的等差数列,偶数列是以s为首项,以a为公差的等差数列,由此能求出数列{an}的通项公式.
(2)由递推公式求出a1=1,a2=3,a3=2a+b-3,a4=a+3,由此利用等差数列性质能求出a=4,b=0,从而得到数列{an}是首项为2,公差为2的等差数列,由此能求了Sn.
(3)由已知得a2k+1-a2k=(t+ka)-[s+(k-1)a]=t-s+a>0,由经能求出a的取值范围.
解答 证明:(1)∵数列{an}满足:a1=t,a2=s且an+an+1=an+b对于n∈N*恒成立,
∴an+1=an+b-an,
an+2=a(n+1)+b-an+1=(an+a+b)-(an+b)+an=a+an,
∴an+2-an=a,
∴数列{an}是“弱等差数列”.
∵a1=t,a2=s,an+2-an=a,
∴{an}中奇数项是以t为首项,以a为公差的等差数列,偶数列是以s为首项,以a为公差的等差数列,
∴an=$\left\{\begin{array}{l}{t+\frac{n-1}{2}a,n为奇数}\\{s+(\frac{n}{2}-1)a,n为偶数}\end{array}\right.$.
解:(2)∵当t=1,s=3时,数列{an}是等差数列,
∴a1=1,a2=3,3+a3=2a+b,
∴a3=2a+b-3,2a+b-3+a4=3a+b,∴a4=a+3,
∴$\left\{\begin{array}{l}{{a}_{3}-{a}_{2}=2a+b-3-3=2}\\{{a}_{4}-{a}_{3}=a+3-2a-b+3=2}\end{array}\right.$,解得a=4,b=0,
∴数列{an}是首项为2,公差为2的等差数列,
∴Sn=2n+$\frac{n(n-1)}{2}×2$=n2+n.
(3)∵s>t,且数列{an}是单调递增数列,
∴a2k+1-a2k=(t+ka)-[s+(k-1)a]=t-s+a>0,
∴a>s-t.
∴a的取值范围是(s-t,+∞).
点评 本题考查“弱等差数列”的证明,考查数列的通项公式的求法,综合性质强,难度大,解题时要认真审题,注意等差数列的性质的合理运用.

| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
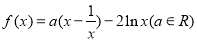 ,
,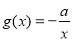 ,若至少存在一个
,若至少存在一个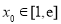 ,使
,使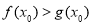 成立,则实数a的范围为( )
成立,则实数a的范围为( )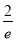 ,+∞) B.(0,+∞)
,+∞) B.(0,+∞)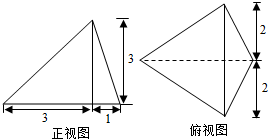
 是函数
是函数 的极小值点,则
的极小值点,则 =( )
=( )